Quasi-Monte-Carlo#

Bevor wir uns mit Quasi-Monte Carlo (QMC) befassen, eine kurze Einführung in Monte Carlo (MC). MC-Methoden oder MC-Experimente sind eine breite Klasse von rechnerischen Algorithmen, die auf wiederholter Zufallsstichproben beruhen, um numerische Ergebnisse zu erzielen. Das zugrundeliegende Konzept besteht darin, Zufälligkeit zu nutzen, um Probleme zu lösen, die prinzipiell deterministisch sein könnten. Sie werden häufig in physikalischen und mathematischen Problemen eingesetzt und sind am nützlichsten, wenn andere Ansätze schwierig oder unmöglich sind. MC-Methoden werden hauptsächlich in drei Problemklassen eingesetzt: Optimierung, numerische Integration und Erzeugung von Stichproben aus einer Wahrscheinlichkeitsverteilung.

Das Erzeugen von Zufallszahlen mit spezifischen Eigenschaften ist ein komplexeres Problem, als es klingt. Einfache MC-Methoden sind darauf ausgelegt, Punkte unabhängig und identisch verteilt (IID) zu erzeugen. Aber die Erzeugung mehrerer Sätze von Zufallspunkten kann zu radikal unterschiedlichen Ergebnissen führen.

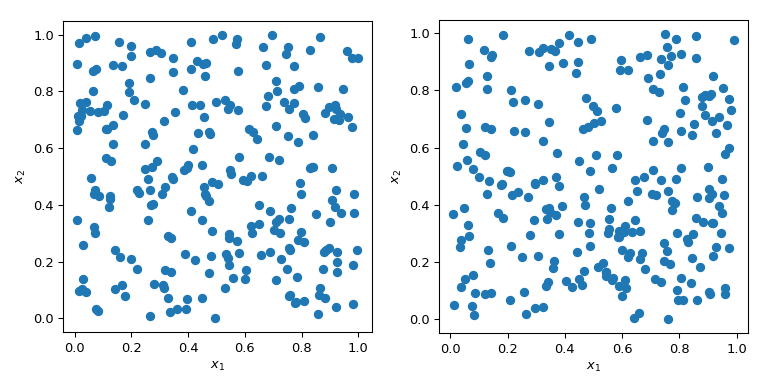
In beiden Fällen der obigen Abbildung werden Punkte zufällig ohne Kenntnis der zuvor gezogenen Punkte erzeugt. Es ist klar, dass einige Regionen des Raumes unerforscht bleiben – was in Simulationen zu Problemen führen kann, da ein bestimmter Satz von Punkten ein völlig anderes Verhalten auslösen könnte.

Ein großer Vorteil von MC ist, dass es bekannte Konvergenzeigenschaften hat. Betrachten wir den Mittelwert der quadrierten Summe in 5 Dimensionen

\[f(\mathbf{x}) = \left( \sum_{j=1}^{5}x_j \right)^2,\]

mit \(x_j \sim \mathcal{U}(0,1)\). Er hat einen bekannten Mittelwert, \(\mu = 5/3+5(5-1)/4\). Mittels MC-Stichproben können wir diesen Mittelwert numerisch berechnen, und der Approximationsfehler folgt einer theoretischen Rate von \(O(n^{-1/2})\).

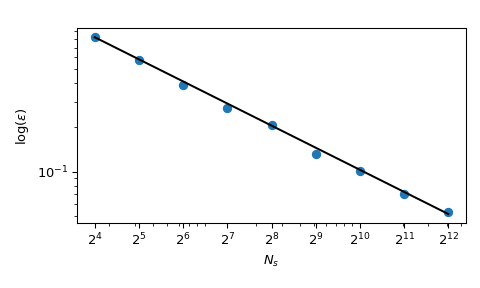
Obwohl die Konvergenz gewährleistet ist, tendieren Praktiker dazu, einen explorativen Prozess zu wünschen, der deterministischer ist. Mit normalem MC kann ein Seed verwendet werden, um einen wiederholbaren Prozess zu haben. Aber das Festlegen des Seeds würde die Konvergenzeigenschaft brechen: Ein bestimmter Seed könnte für eine bestimmte Klasse von Problemen funktionieren und für eine andere versagen.

Was üblicherweise getan wird, um den Raum auf deterministische Weise zu durchlaufen, ist die Verwendung eines regelmäßigen Gitters, das alle Parameterdimensionen abdeckt, auch als gesättigtes Design bezeichnet. Betrachten wir den Einheits-Hyperwürfel, bei dem alle Grenzen von 0 bis 1 reichen. Wenn nun ein Abstand von 0,1 zwischen den Punkten liegt, wären 10 Punkte erforderlich, um das Einheitsintervall zu füllen. In einem 2-dimensionalen Hyperwürfel würde derselbe Abstand 100 Punkte erfordern, und in 3 Dimensionen 1.000 Punkte. Mit zunehmender Anzahl von Dimensionen steigt die Anzahl der Experimente, die zur Füllung des Raumes erforderlich sind, exponentiell mit der Dimensionalität des Raumes. Dieses exponentielle Wachstum wird als „Fluch der Dimensionalität“ bezeichnet.

>>> import numpy as np
>>> disc = 10
>>> x1 = np.linspace(0, 1, disc)
>>> x2 = np.linspace(0, 1, disc)
>>> x3 = np.linspace(0, 1, disc)
>>> x1, x2, x3 = np.meshgrid(x1, x2, x3)

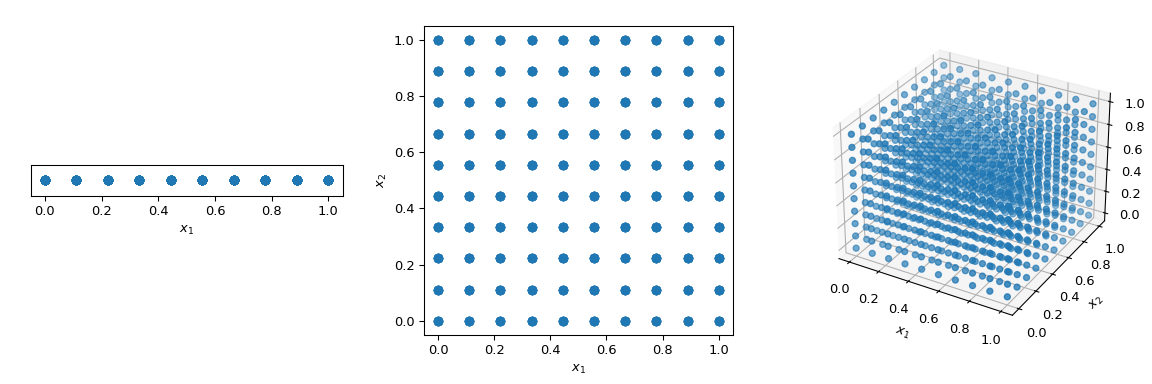
Um dieses Problem zu mildern, wurden QMC-Methoden entwickelt. Sie sind deterministisch, haben eine gute Abdeckung des Raumes und einige von ihnen können fortgesetzt werden und gute Eigenschaften beibehalten. Der Hauptunterschied zu MC-Methoden besteht darin, dass die Punkte nicht IID sind, sondern Kenntnis von früheren Punkten haben. Daher werden einige Methoden auch als Sequenzen bezeichnet.

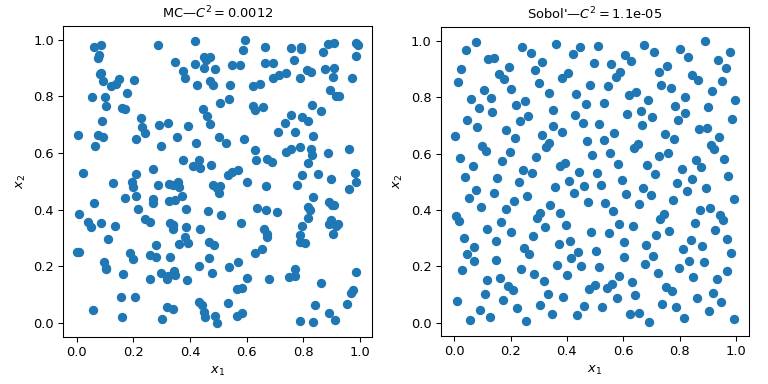
Diese Abbildung zeigt 2 Sätze von 256 Punkten. Das Design auf der linken Seite ist ein einfaches MC, während das Design auf der rechten Seite ein QMC-Design mit der Sobol’-Methode ist. Wir sehen deutlich, dass die QMC-Version gleichmäßiger ist. Die Punkte beproben die Grenzen besser und es gibt weniger Cluster oder Lücken.

Eine Möglichkeit, die Gleichmäßigkeit zu beurteilen, ist die Verwendung eines Maßes namens Diskrepanz. Hier ist die Diskrepanz von Sobol’-Punkten besser als bei rohem MC.

Zurück zur Berechnung des Mittelwerts haben QMC-Methoden auch bessere Konvergenzraten für den Fehler. Sie können für diese Funktion \(O(n^{-1})\) erreichen, und sogar bessere Raten für sehr glatte Funktionen. Diese Abbildung zeigt, dass die Sobol’-Methode eine Rate von \(O(n^{-1})\) hat

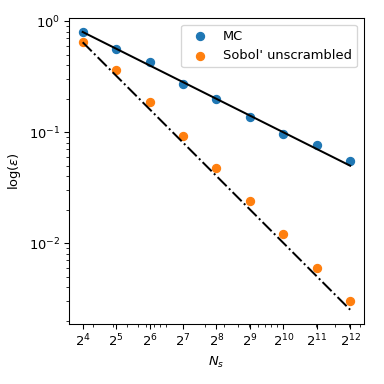
Für weitere mathematische Details verweisen wir auf die Dokumentation von scipy.stats.qmc.

Berechnung der Diskrepanz#

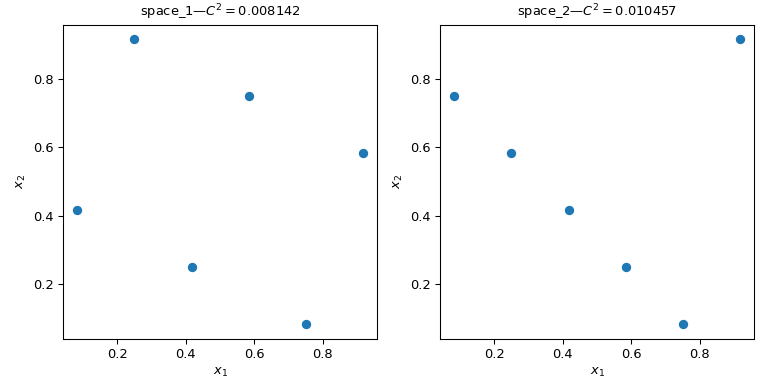
Betrachten wir zwei Sätze von Punkten. Aus der folgenden Abbildung ist klar ersichtlich, dass das Design auf der linken Seite mehr Raum abdeckt als das Design auf der rechten Seite. Dies kann mit einem scipy.stats.qmc.discrepancy-Maß quantifiziert werden. Je niedriger die Diskrepanz, desto gleichmäßiger ist eine Stichprobe.

>>> import numpy as np
>>> from scipy.stats import qmc
>>> space_1 = np.array([[1, 3], [2, 6], [3, 2], [4, 5], [5, 1], [6, 4]])
>>> space_2 = np.array([[1, 5], [2, 4], [3, 3], [4, 2], [5, 1], [6, 6]])
>>> l_bounds = [0.5, 0.5]
>>> u_bounds = [6.5, 6.5]
>>> space_1 = qmc.scale(space_1, l_bounds, u_bounds, reverse=True)
>>> space_2 = qmc.scale(space_2, l_bounds, u_bounds, reverse=True)
>>> qmc.discrepancy(space_1)
0.008142039609053464
>>> qmc.discrepancy(space_2)
0.010456854423869011

Verwendung einer QMC-Engine#

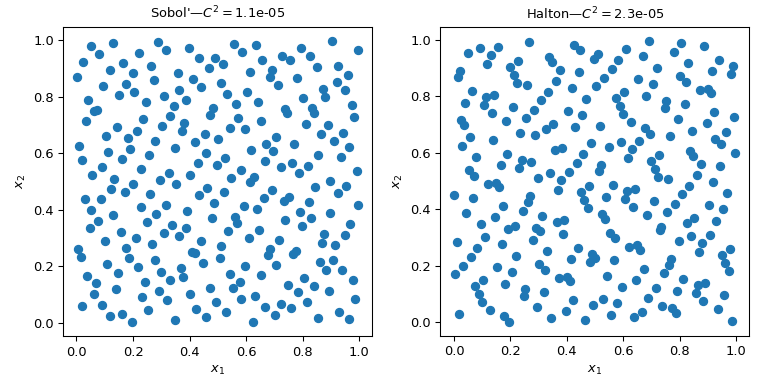
Mehrere QMC-Sampler/Engines sind implementiert. Hier betrachten wir zwei der am häufigsten verwendeten QMC-Methoden: scipy.stats.qmc.Sobol und scipy.stats.qmc.Halton Sequenzen.

"""Sobol' and Halton sequences."""
from scipy.stats import qmc
import numpy as np

import matplotlib.pyplot as plt


rng = np.random.default_rng()

n_sample = 256
dim = 2

sample = {}

# Sobol'
engine = qmc.Sobol(d=dim, seed=rng)
sample["Sobol'"] = engine.random(n_sample)

# Halton
engine = qmc.Halton(d=dim, seed=rng)
sample["Halton"] = engine.random(n_sample)

fig, axs = plt.subplots(1, 2, figsize=(8, 4))

for i, kind in enumerate(sample):
    axs[i].scatter(sample[kind][:, 0], sample[kind][:, 1])

    axs[i].set_aspect('equal')
    axs[i].set_xlabel(r'$x_1$')
    axs[i].set_ylabel(r'$x_2$')
    axs[i].set_title(f'{kind}—$C^2 = ${qmc.discrepancy(sample[kind]):.2}')

plt.tight_layout()
plt.show()

Warnung

QMC-Methoden erfordern besondere Sorgfalt, und der Benutzer muss die Dokumentation lesen, um gängige Fallstricke zu vermeiden. Sobol’ erfordert zum Beispiel eine Anzahl von Punkten, die eine Potenz von 2 ist. Auch das Ausdünnen, Brennen oder andere Punktselektionen können die Eigenschaften der Sequenz zerstören und zu einem Satz von Punkten führen, der nicht besser ist als MC.

QMC-Engines sind zustandsbewusst. Das bedeutet, dass Sie die Sequenz fortsetzen, einige Punkte überspringen oder sie zurücksetzen können. Nehmen wir 5 Punkte von scipy.stats.qmc.Halton. Und dann bitten wir um einen zweiten Satz von 5 Punkten

>>> from scipy.stats import qmc
>>> engine = qmc.Halton(d=2)
>>> engine.random(5)
array([[0.22166437, 0.07980522],  # random
       [0.72166437, 0.93165708],
       [0.47166437, 0.41313856],
       [0.97166437, 0.19091633],
       [0.01853937, 0.74647189]])
>>> engine.random(5)
array([[0.51853937, 0.52424967],  # random
       [0.26853937, 0.30202745],
       [0.76853937, 0.857583  ],
       [0.14353937, 0.63536078],
       [0.64353937, 0.01807683]])

Nun setzen wir die Sequenz zurück. Wenn wir nach 5 Punkten fragen, erhalten wir dieselben ersten 5 Punkte

>>> engine.reset()
>>> engine.random(5)
array([[0.22166437, 0.07980522],  # random
       [0.72166437, 0.93165708],
       [0.47166437, 0.41313856],
       [0.97166437, 0.19091633],
       [0.01853937, 0.74647189]])

Und hier schreiten wir in der Sequenz voran, um denselben zweiten Satz von 5 Punkten zu erhalten

>>> engine.reset()
>>> engine.fast_forward(5)
>>> engine.random(5)
array([[0.51853937, 0.52424967],  # random
       [0.26853937, 0.30202745],
       [0.76853937, 0.857583  ],
       [0.14353937, 0.63536078],
       [0.64353937, 0.01807683]])

Hinweis

Standardmäßig sind sowohl scipy.stats.qmc.Sobol als auch scipy.stats.qmc.Halton gemischt (scrambled). Die Konvergenzeigenschaften sind besser, und es verhindert das Auftreten von Streifen oder auffälligen Mustern von Punkten in hohen Dimensionen. Es sollte keinen praktischen Grund geben, die gemischte Version nicht zu verwenden.

Erstellen einer QMC-Engine, d.h. Unterklassenbildung von `QMCEngine`#

Um Ihre eigene scipy.stats.qmc.QMCEngine zu erstellen, müssen einige Methoden definiert werden. Im Folgenden finden Sie ein Beispiel, das numpy.random.Generator umschließt.

>>> import numpy as np
>>> from scipy.stats import qmc
>>> class RandomEngine(qmc.QMCEngine):
...     def __init__(self, d, seed=None):
...         super().__init__(d=d, seed=seed)
...         self.rng = np.random.default_rng(self.rng_seed)
...
...
...     def _random(self, n=1, *, workers=1):
...         return self.rng.random((n, self.d))
...
...
...     def reset(self):
...         self.rng = np.random.default_rng(self.rng_seed)
...         self.num_generated = 0
...         return self
...
...
...     def fast_forward(self, n):
...         self.random(n)
...         return self

Dann verwenden wir sie wie jede andere QMC-Engine

>>> engine = RandomEngine(2)
>>> engine.random(5)
array([[0.22733602, 0.31675834],  # random
       [0.79736546, 0.67625467],
       [0.39110955, 0.33281393],
       [0.59830875, 0.18673419],
       [0.67275604, 0.94180287]])
>>> engine.reset()
>>> engine.random(5)
array([[0.22733602, 0.31675834],  # random
       [0.79736546, 0.67625467],
       [0.39110955, 0.33281393],
       [0.59830875, 0.18673419],
       [0.67275604, 0.94180287]])

Richtlinien zur Verwendung von QMC#

QMC hat Regeln! Stellen Sie sicher, dass Sie die Dokumentation lesen, sonst haben Sie keinen Vorteil gegenüber MC.
Verwenden Sie scipy.stats.qmc.Sobol, wenn Sie **genau** \(2^m\) Punkte benötigen.
scipy.stats.qmc.Halton ermöglicht das Beproben oder Überspringen einer beliebigen Anzahl von Punkten. Dies geschieht auf Kosten einer langsameren Konvergenzrate als bei Sobol’.
Entfernen Sie niemals die ersten Punkte der Sequenz. Dies zerstört die Eigenschaften.
Mischen ist immer besser.
Wenn Sie LHS-basierte Methoden verwenden, können Sie keine Punkte hinzufügen, ohne die LHS-Eigenschaften zu verlieren. (Es gibt einige Methoden, dies zu tun, aber diese sind nicht implementiert.)

Quasi-Monte-Carlo#

Berechnung der Diskrepanz#

Verwendung einer QMC-Engine#

Erstellen einer QMC-Engine, d.h. Unterklassenbildung von QMCEngine#

Richtlinien zur Verwendung von QMC#

Erstellen einer QMC-Engine, d.h. Unterklassenbildung von `QMCEngine`#