UnivariateSpline#
- class scipy.interpolate.UnivariateSpline(x, y, w=None, bbox=[None, None], k=3, s=None, ext=0, check_finite=False)[Quelle]#
1-D-Glättungs-Spline-Anpassung an einen gegebenen Satz von Datenpunkten.
Veraltet
Diese Klasse gilt als veraltet und wird keine Updates mehr erhalten. Obwohl wir derzeit keine Pläne haben, sie zu entfernen, empfehlen wir, dass neuer Code stattdessen modernere Alternativen verwendet. Insbesondere empfehlen wir die Verwendung von
make_splrep.Passt einen Spline y = spl(x) des Grades k an die bereitgestellten x, y-Daten an. s gibt die Anzahl der Knoten an, indem eine Glättungsbedingung spezifiziert wird.
- Parameter:
- x(N,) array_like
1-D-Array von unabhängigen Eingabedaten. Muss steigend sein; muss streng steigend sein, wenn s 0 ist.
- y(N,) array_like
1-D-Array von abhängigen Eingabedaten, mit der gleichen Länge wie x.
- w(N,) array_like, optional
Gewichte für die Spline-Anpassung. Müssen positiv sein. Wenn w None ist, sind die Gewichte alle 1. Standard ist None.
- bbox(2,) array_like, optional
2-Sequenz, die die Grenze des Approximationsintervalls angibt. Wenn bbox None ist, dann
bbox=[x[0], x[-1]]. Standard ist None.- kint, optional
Grad des Glättungs-Splines. Muss 1 <= k <= 5 sein.
k = 3ist ein kubischer Spline. Standard ist 3.- sfloat oder None, optional
Positiver Glättungsfaktor, der zur Auswahl der Anzahl der Knoten verwendet wird. Die Anzahl der Knoten wird erhöht, bis die Glättungsbedingung erfüllt ist.
sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) <= s
Aufgrund von numerischen Problemen ist die tatsächliche Bedingung jedoch:
abs(sum((w[i] * (y[i]-spl(x[i])))**2, axis=0) - s) < 0.001 * s
Wenn s None ist, wird s auf len(w) für einen Glättungs-Spline gesetzt, der alle Datenpunkte verwendet. Wenn 0, interpoliert der Spline durch alle Datenpunkte. Dies ist äquivalent zu
InterpolatedUnivariateSpline. Standard ist None. Der Benutzer kann s verwenden, um den Kompromiss zwischen Nähe und Glattheit der Anpassung zu steuern. Größeres s bedeutet mehr Glättung, während kleinere Werte von s weniger Glättung bedeuten. Empfohlene Werte für s hängen von den Gewichten w ab. Wenn die Gewichte die Inverse der Standardabweichung von y darstellen, dann sollte ein guter s-Wert im Bereich (m-sqrt(2*m),m+sqrt(2*m)) liegen, wobei m die Anzahl der Datenpunkte in x, y und w ist. Das bedeutet, dasss = len(w)ein guter Wert ist, wenn1/w[i]eine Schätzung der Standardabweichung vony[i]ist.- extint oder str, optional
Steuert den Extrapolationsmodus für Elemente, die nicht im Intervall der Knotensequenz liegen.
wenn ext=0 oder „extrapolate“, gib den extrapolierten Wert zurück.
wenn ext=1 oder „zeros“, gib 0 zurück.
wenn ext=2 oder „raise“, löse einen ValueError aus.
wenn ext=3 oder „const“, gib den Grenzwert zurück.
Standard ist 0.
- check_finitebool, optional
Ob geprüft werden soll, ob die Eingabearrays nur endliche Zahlen enthalten. Deaktivierung kann die Leistung verbessern, kann aber zu Problemen (Abstürze, Nicht-Terminierung oder unsinnige Ergebnisse) führen, wenn die Eingaben Unendlichkeiten oder NaNs enthalten. Standard ist False.
Methoden
__call__(x[, nu, ext])Bewerte den Spline (oder seine nu-te Ableitung) an den Positionen x.
antiderivative([n])Konstruiere einen neuen Spline, der die Stammfunktion dieses Splines darstellt.
derivative([n])Konstruiere einen neuen Spline, der die Ableitung dieses Splines darstellt.
derivatives(x)Gib alle Ableitungen des Splines an der Stelle x zurück.
Gib die Spline-Koeffizienten zurück.
Gib die Positionen der inneren Knoten des Splines zurück.
Gib die gewichtete Summe der quadrierten Residuen der Spline-Approximation zurück.
integral(a, b)Gib das bestimmte Integral des Splines zwischen zwei gegebenen Punkten zurück.
roots()Gib die Nullstellen des Splines zurück.
Fahre die Spline-Berechnung mit dem gegebenen Glättungsfaktor s und den bei der letzten Aufruf gefundenen Knoten fort.
validate_input
Siehe auch
BivariateSplineEine Basisklasse für bivariate Splines.
SmoothBivariateSplineEin glättender bivariate Spline durch die gegebenen Punkte
LSQBivariateSplineEin bivariate Spline unter Verwendung von gewichteter Kleinster-Quadrate-Anpassung
RectSphereBivariateSplineEin bivariate Spline über ein rechteckiges Gitter auf einer Kugel
SmoothSphereBivariateSplineEin glättender bivariate Spline in Kugelkoordinaten
LSQSphereBivariateSplineEin bivariate Spline in Kugelkoordinaten unter Verwendung von gewichteter Kleinster-Quadrate-Anpassung
RectBivariateSplineEin bivariate Spline über ein rechteckiges Gitter
InterpolatedUnivariateSplineEin interpolierender univarianter Spline für einen gegebenen Satz von Datenpunkten.
bisplrepEine Funktion zum Finden einer B-Spline-Darstellung einer Oberfläche im Bivariaten
bisplevEine Funktion zur Auswertung eines B-Splines im Bivariaten und seiner Ableitungen
splrepEine Funktion zum Finden der B-Spline-Darstellung einer 1-D-Kurve
splevEine Funktion zur Auswertung eines B-Splines oder seiner Ableitungen
sprootEine Funktion zum Finden der Nullstellen eines kubischen B-Splines
splintEine Funktion zur Auswertung des bestimmten Integrals eines B-Splines zwischen zwei gegebenen Punkten
spaldeEine Funktion zur Auswertung aller Ableitungen eines B-Splines
Hinweise
Die Anzahl der Datenpunkte muss größer sein als der Spline-Grad k.
NaN-Handhabung: Wenn die Eingabearrays
nan-Werte enthalten, ist das Ergebnis nicht nützlich, da die zugrunde liegenden Spline-Anpassungsroutinen nicht mitnanumgehen können. Eine Umgehung besteht darin, Nullgewichte für Not-a-Number-Datenpunkte zu verwenden.>>> import numpy as np >>> from scipy.interpolate import UnivariateSpline >>> x, y = np.array([1, 2, 3, 4]), np.array([1, np.nan, 3, 4]) >>> w = np.isnan(y) >>> y[w] = 0. >>> spl = UnivariateSpline(x, y, w=~w)
Beachten Sie die Notwendigkeit, ein
nandurch einen numerischen Wert zu ersetzen (der genaue Wert spielt keine Rolle, solange das entsprechende Gewicht null ist).Referenzen
Basierend auf Algorithmen beschrieben in [1], [2], [3] und [4]
[1]P. Dierckx, „An algorithm for smoothing, differentiation and integration of experimental data using spline functions“, J.Comp.Appl.Maths 1 (1975) 165-184.
[2]P. Dierckx, „A fast algorithm for smoothing data on a rectangular grid while using spline functions“, SIAM J.Numer.Anal. 19 (1982) 1286-1304.
[3]P. Dierckx, „An improved algorithm for curve fitting with spline functions“, report tw54, Dept. Computer Science,K.U.Leuven, 1981.
[4]P. Dierckx, “Curve and surface fitting with splines”, Monographs on Numerical Analysis, Oxford University Press, 1993.
Beispiele
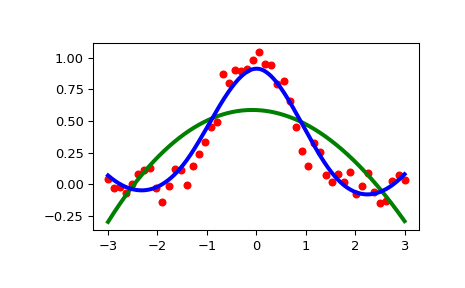
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import UnivariateSpline >>> rng = np.random.default_rng() >>> x = np.linspace(-3, 3, 50) >>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(50) >>> plt.plot(x, y, 'ro', ms=5)
Verwenden Sie den Standardwert für den Glättungsparameter
>>> spl = UnivariateSpline(x, y) >>> xs = np.linspace(-3, 3, 1000) >>> plt.plot(xs, spl(xs), 'g', lw=3)
Ändern Sie manuell den Grad der Glättung
>>> spl.set_smoothing_factor(0.5) >>> plt.plot(xs, spl(xs), 'b', lw=3) >>> plt.show()