scipy.interpolate.

spalde

scipy.interpolate.spalde(x, tck)

Wertet eine B-Spline und alle ihre Ableitungen an einem Punkt (oder einer Menge von Punkten) bis zur Ordnung k (dem Grad der Spline) aus, wobei 0 die Spline selbst ist.

Veraltet

Diese Funktion gilt als veraltet und wird keine Updates mehr erhalten. Obwohl wir derzeit keine Pläne haben, sie zu entfernen, empfehlen wir, dass neuer Code modernere Alternativen verwendet. Insbesondere empfehlen wir, ein BSpline-Objekt zu konstruieren und seine Ableitung in einer Schleife oder einer Listenkomprehension auszuwerten.

Parameter:

xarray_like

Ein Punkt oder eine Menge von Punkten, an denen die Ableitungen ausgewertet werden sollen. Beachten Sie, dass für jedes x t(k) <= x <= t(n-k+1) gelten muss.

tcktuple

Ein Tupel (t,c,k), das den Vektor der Knoten, die B-Spline-Koeffizienten und den Grad der Spline enthält, deren Ableitungen berechnet werden sollen.

Rückgabe:

Ergebnisse{ndarray, Liste von ndarrays}

Ein Array (oder eine Liste von Arrays), das alle Ableitungen bis einschließlich Ordnung k für jeden Punkt x enthält, wobei das erste Element die Spline selbst ist.

Siehe auch

splprep, splrep, splint, sproot, splev, bisplrep, bisplev

UnivariateSpline, BivariateSpline

Referenzen

[1]

de Boor C : On calculating with b-splines, J. Approximation Theory 6 (1972) 50-62.

[2]

Cox M.G. : The numerical evaluation of b-splines, J. Inst. Maths applics 10 (1972) 134-149.

[3]

Dierckx P. : Curve and surface fitting with splines, Monographs on Numerical Analysis, Oxford University Press, 1993.

Beispiele

Probieren Sie es in Ihrem Browser aus!

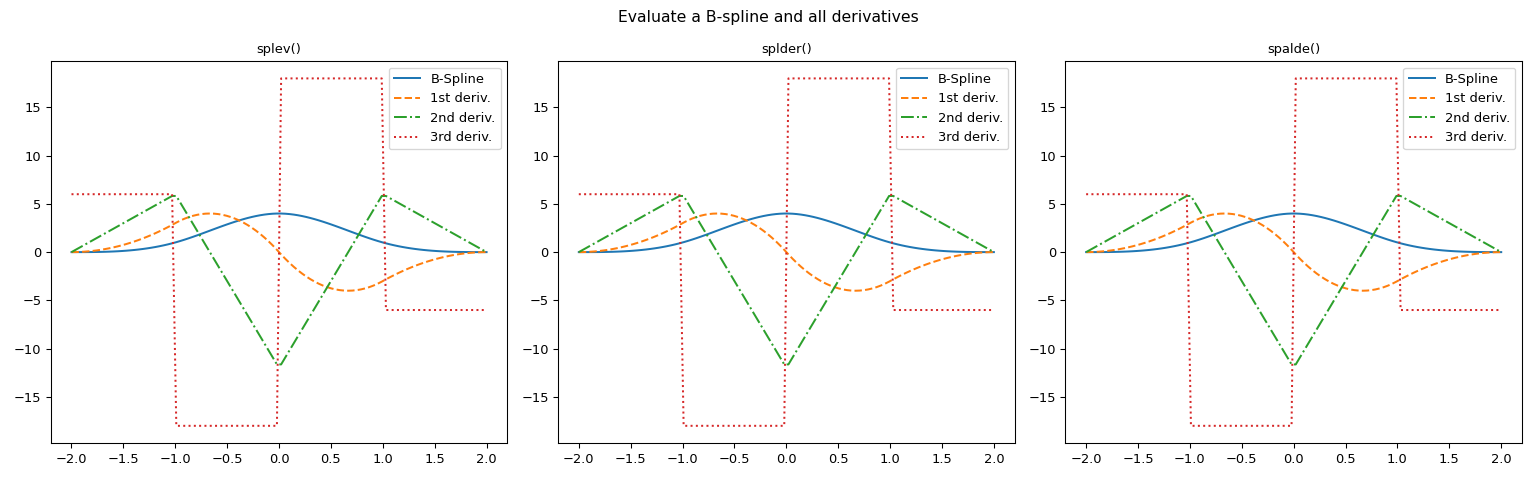
Um die Ableitungen einer B-Spline zu berechnen, gibt es mehrere Ansätze. In diesem Beispiel zeigen wir, dass spalde äquivalent zum Aufruf von splev und splder ist.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import BSpline, spalde, splder, splev

>>> # Store characteristic parameters of a B-spline
>>> tck = ((-2, -2, -2, -2, -1, 0, 1, 2, 2, 2, 2),  # knots
...        (0, 0, 0, 6, 0, 0, 0),  # coefficients
...        3)  # degree (cubic)
>>> # Instance a B-spline object
>>> # `BSpline` objects are preferred, except for spalde()
>>> bspl = BSpline(tck[0], tck[1], tck[2])
>>> # Generate extra points to get a smooth curve
>>> x = np.linspace(min(tck[0]), max(tck[0]), 100)

Kurve und alle Ableitungen auswerten

>>> # The order of derivative must be less or equal to k, the degree of the spline
>>> # Method 1: spalde()
>>> f1_y_bsplin = [spalde(i, tck)[0] for i in x ]  # The B-spline itself
>>> f1_y_deriv1 = [spalde(i, tck)[1] for i in x ]  # 1st derivative
>>> f1_y_deriv2 = [spalde(i, tck)[2] for i in x ]  # 2nd derivative
>>> f1_y_deriv3 = [spalde(i, tck)[3] for i in x ]  # 3rd derivative
>>> # You can reach the same result by using `splev`and `splder`
>>> f2_y_deriv3 = splev(x, bspl, der=3)
>>> f3_y_deriv3 = splder(bspl, n=3)(x)

>>> # Generate a figure with three axes for graphic comparison
>>> fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(16, 5))
>>> suptitle = fig.suptitle(f'Evaluate a B-spline and all derivatives')
>>> # Plot B-spline and all derivatives using the three methods
>>> orders = range(4)
>>> linetypes = ['-', '--', '-.', ':']
>>> labels = ['B-Spline', '1st deriv.', '2nd deriv.', '3rd deriv.']
>>> functions = ['splev()', 'splder()', 'spalde()']
>>> for order, linetype, label in zip(orders, linetypes, labels):
...     ax1.plot(x, splev(x, bspl, der=order), linetype, label=label)
...     ax2.plot(x, splder(bspl, n=order)(x), linetype, label=label)
...     ax3.plot(x, [spalde(i, tck)[order] for i in x], linetype, label=label)
>>> for ax, function in zip((ax1, ax2, ax3), functions):
...     ax.set_title(function)
...     ax.legend()
>>> plt.tight_layout()
>>> plt.show()

ZurückIn Tab öffnen