scipy.interpolate.

splprep#

scipy.interpolate.splprep(x, w=None, u=None, ub=None, ue=None, k=3, task=0, s=None, t=None, full_output=0, nest=None, per=0, quiet=1)[Quelle]#

Finden Sie die B-Spline-Darstellung einer N-dimensionalen Kurve.

Veraltet

Diese Funktion gilt als veraltet und wird keine Updates mehr erhalten. Obwohl wir derzeit keine Pläne haben, sie zu entfernen, empfehlen wir, dass neuer Code stattdessen modernere Alternativen verwendet. Insbesondere empfehlen wir, in neuem Code make_splprep zu verwenden.

Finden Sie eine glatte, approximierende Spline-Kurve g(u), gegeben eine Liste von N Rang-1-Arrays, x, die eine parametrisierte Kurve im N-dimensionalen Raum u darstellen. Verwendet die FORTRAN-Routine parcur aus FITPACK.

Parameter:

xarray_like: Eine Liste von Vektor-Arrays, die die Kurve repräsentieren.
warray_like, optional: Streng positive Rang-1-Arrays von Gewichten gleicher Länge wie x[0]. Die Gewichte werden bei der Berechnung der gewichteten Spline-Anpassung nach kleinsten Quadraten verwendet. Wenn die Fehler in den x-Werten die Standardabweichung d haben, dann sollte w gleich 1/d sein. Standardmäßig ones(len(x[0])).
uarray_like, optional: Ein Array von Parameterwerten. Wenn nicht angegeben, werden diese Werte automatisch berechnet als M = len(x[0]), wobei

v[0] = 0

v[i] = v[i-1] + distance(x[i], x[i-1])

u[i] = v[i] / v[M-1]
ub, ueint, optional: Die Endpunkte des Parameterintervalls. Standardmäßig u[0] und u[-1].
kint, optional: Grad des Splines. Kubische Splines werden empfohlen. Gerade Werte von k sollten besonders bei kleinem s-Wert vermieden werden. 1 <= k <= 5, Standard ist 3.
taskint, optional: Wenn task==0 (Standard), finden Sie t und c für einen gegebenen Glättungsfaktor s. Wenn task==1, finden Sie t und c für einen anderen Wert des Glättungsfaktors s. Es muss ein vorheriger Aufruf mit task=0 oder task=1 für denselben Datensatz erfolgt sein. Wenn task=-1, finden Sie die gewichtete Spline-Anpassung nach kleinsten Quadraten für einen gegebenen Satz von Knoten, t.
sfloat, optional: Eine Glättungsbedingung. Das Ausmaß der Glättung wird durch die Erfüllung der folgenden Bedingungen bestimmt: sum((w * (y - g))**2,axis=0) <= s, wobei g(x) die geglättete Interpolation von (x,y) ist. Der Benutzer kann s verwenden, um den Kompromiss zwischen Nähe und Glattheit der Anpassung zu steuern. Größeres s bedeutet mehr Glättung, während kleinere Werte von s weniger Glättung anzeigen. Empfohlene Werte für s hängen von den Gewichten w ab. Wenn die Gewichte die Umkehrung der Standardabweichung von y darstellen, dann sollte ein guter s-Wert im Bereich (m-sqrt(2*m),m+sqrt(2*m)) liegen, wobei m die Anzahl der Datenpunkte in x, y und w ist.
tarray, optional: Die Knoten, die für task=-1 benötigt werden. Es müssen mindestens 2*k+2 Knoten vorhanden sein.
full_outputint, optional: Wenn ungleich Null, werden optionale Ausgaben zurückgegeben.
nestint, optional: Eine Überschätzung der Gesamtzahl der Knoten des Splines, um bei der Bestimmung des Speicherplatzes zu helfen. Standardmäßig nest=m/2. Immer ausreichend groß ist nest=m+k+1.
perint, optional: Wenn ungleich Null, werden die Datenpunkte als periodisch mit der Periode x[m-1] - x[0] betrachtet und eine glatte, periodische Spline-Approximation wird zurückgegeben. Die Werte von y[m-1] und w[m-1] werden nicht verwendet.
quietint, optional: Ungleich Null, um Meldungen zu unterdrücken.

Rückgabe:

tcktuple: Ein Tupel, (t,c,k), das den Vektor der Knoten, die B-Spline-Koeffizienten und den Grad des Splines enthält.
uarray: Ein Array der Werte des Parameters.
fpfloat: Die gewichtete Summe der quadrierten Residuen der Spline-Approximation.
ierint: Ein Integer-Flag für den Erfolg von splrep. Erfolg wird angezeigt, wenn ier<=0. Wenn ier in [1,2,3] ein Fehler aufgetreten ist, aber nicht gemeldet wurde. Andernfalls wird ein Fehler gemeldet.
msgstr: Eine Nachricht, die dem Integer-Flag ier entspricht.

Siehe auch

splrep, splev, sproot, spalde, splint
bisplrep, bisplev
UnivariateSpline, BivariateSpline
BSpline
make_interp_spline

Hinweise

Siehe splev zur Auswertung des Splines und seiner Ableitungen. Die Anzahl der Dimensionen N muss kleiner als 11 sein.

Die Anzahl der Koeffizienten im Array c ist k+1 weniger als die Anzahl der Knoten len(t). Dies steht im Gegensatz zu splrep, welches das Array der Koeffizienten mit Nullen auffüllt, um die gleiche Länge wie das Array der Knoten zu haben. Diese zusätzlichen Koeffizienten werden von den Auswertungsroutinen splev und BSpline ignoriert.

Referenzen

[1]

P. Dierckx, “Algorithms for smoothing data with periodic and parametric splines, Computer Graphics and Image Processing”, 20 (1982) 171-184.

[2]

P. Dierckx, „Algorithms for smoothing data with periodic and parametric splines“, report tw55, Dept. Computer Science, K.U.Leuven, 1981.

[3]

P. Dierckx, “Curve and surface fitting with splines”, Monographs on Numerical Analysis, Oxford University Press, 1993.

Beispiele

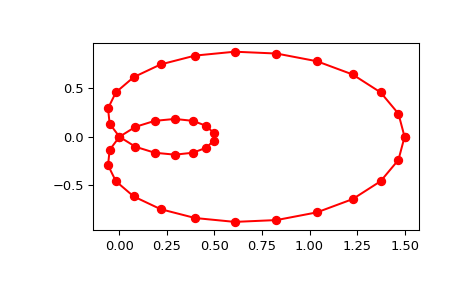
Generieren Sie eine Diskretisierung einer Limacon-Kurve in Polarkoordinaten

>>> import numpy as np
>>> phi = np.linspace(0, 2.*np.pi, 40)
>>> r = 0.5 + np.cos(phi)         # polar coords
>>> x, y = r * np.cos(phi), r * np.sin(phi)    # convert to cartesian

Und interpolieren

>>> from scipy.interpolate import splprep, splev
>>> tck, u = splprep([x, y], s=0)
>>> new_points = splev(u, tck)

Beachten Sie, dass (i) wir die Interpolation erzwingen, indem wir s=0 verwenden, (ii) die Parametrisierung u automatisch generiert wird. Plotten Sie nun das Ergebnis

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y, 'ro')
>>> ax.plot(new_points[0], new_points[1], 'r-')
>>> plt.show()

../../_images/scipy-interpolate-splprep-1.png