scipy.spatial.transform.

Rotation#

class scipy.spatial.transform.Rotation#

Rotation in 3 Dimensionen.

Diese Klasse bietet eine Schnittstelle zur Initialisierung von und zur Darstellung von Rotationen mit

Quaternionen
Rotationsmatrizen
Rotationsvektoren
Modifizierten Rodrigues-Parametern
Euler-Winkeln
Davenport-Winkeln (Generalisierte Euler-Winkel)

Die folgenden Operationen auf Rotationen werden unterstützt

Anwendung auf Vektoren
Rotationskomposition
Rotationsinversion
Rotationsindizierung

Die Indizierung innerhalb einer Rotation wird unterstützt, da mehrere Rotationstransformationen in einer einzigen Rotation-Instanz gespeichert werden können.

Um Rotation-Objekte zu erstellen, verwenden Sie die from_...-Methoden (siehe Beispiele unten). Rotation(...) soll nicht direkt instanziiert werden.

Attribute:

single: Ob diese Instanz eine einzelne Rotation darstellt.

Methoden

`__len__`(self)	Anzahl der in diesem Objekt enthaltenen Rotationen.
`from_quat`(cls, quat, *[, scalar_first])	Initialisieren aus Quaternionen.
`from_matrix`(cls, matrix)	Initialisieren aus Rotationsmatrix.
`from_rotvec`(cls, rotvec[, degrees])	Initialisieren aus Rotationsvektoren.
`from_mrp`(cls, mrp)	Initialisieren aus Modifizierten Rodrigues-Parametern (MRPs).
`from_euler`(cls, seq, angles[, degrees])	Initialisieren aus Euler-Winkeln.
`from_davenport`(cls, axes, order, angles[, ...])	Initialisieren aus Davenport-Winkeln.
`as_quat`(self[, canonical, scalar_first])	Darstellen als Quaternionen.
`as_matrix`(self)	Darstellen als Rotationsmatrix.
`as_rotvec`(self[, degrees])	Darstellen als Rotationsvektoren.
`as_mrp`(self)	Darstellen als Modifizierte Rodrigues-Parameter (MRPs).
`as_euler`(self, seq[, degrees])	Darstellen als Euler-Winkel.
`as_davenport`(self, axes, order[, degrees])	Darstellen als Davenport-Winkel.
`concatenate`(cls, rotations)	Verketten einer Sequenz von `Rotation`-Objekten zu einem einzigen Objekt.
`apply`(self, vectors[, inverse])	Anwenden dieser Rotation auf eine Menge von Vektoren.
`__mul__`(self, Rotation other)	Komponieren dieser Rotation mit der anderen.
`__pow__`(self, float n, modulus)	Komponieren dieser Rotation mit sich selbst n mal.
`inv`(self)	Invertieren dieser Rotation.
`magnitude`(self)	Ermitteln der Magnitude(n) der Rotation(en).
`approx_equal`(self, Rotation other[, atol, ...])	Feststellen, ob eine andere Rotation dieser ungefähr entspricht.
`mean`(self[, weights])	Ermitteln des Mittelwerts der Rotationen.
`reduce`(self[, left, right, return_indices])	Reduzieren dieser Rotation mit den bereitgestellten Rotationsgruppen.
`create_group`(cls, group[, axis])	Erstellen einer 3D-Rotationsgruppe.
`__getitem__`(self, indexer)	Extrahieren von Rotation(en) an gegebenen Index(en) aus dem Objekt.
`identity`(cls[, num])	Ermitteln von Identitätsrotation(en).
`random`(cls[, num, rng])	Generieren von gleichmäßig verteilten Rotationen.
`align_vectors`(cls, a, b[, weights, ...])	Schätzen einer Rotation zur optimalen Ausrichtung zweier Vektorsätze.

Siehe auch

Slerp

Hinweise

Hinzugefügt in Version 1.2.0.

Beispiele

>>> from scipy.spatial.transform import Rotation as R
>>> import numpy as np

Eine Rotation-Instanz kann in jedem der oben genannten Formate initialisiert und in jedes der anderen konvertiert werden. Das zugrunde liegende Objekt ist unabhängig von der zur Initialisierung verwendeten Darstellung.

Betrachten Sie eine gegen den Uhrzeigersinn gerichtete Drehung um 90 Grad um die z-Achse. Dies entspricht dem folgenden Quaternion (im Skalar-Last-Format)

>>> r = R.from_quat([0, 0, np.sin(np.pi/4), np.cos(np.pi/4)])

Die Drehung kann in jedem der anderen Formate ausgedrückt werden

>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
[ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
[ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

Die gleiche Drehung kann mit einer Rotationsmatrix initialisiert werden

>>> r = R.from_matrix([[0, -1, 0],
...                    [1, 0, 0],
...                    [0, 0, 1]])

Darstellung in anderen Formaten

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

Der Rotationsvektor, der dieser Drehung entspricht, ist gegeben durch

>>> r = R.from_rotvec(np.pi/2 * np.array([0, 0, 1]))

Darstellung in anderen Formaten

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_euler('zyx', degrees=True)
array([90.,  0.,  0.])

Die Methode from_euler ist recht flexibel im Bereich der unterstützten Eingabeformate. Hier initialisieren wir eine einzelne Drehung um eine einzelne Achse

>>> r = R.from_euler('z', 90, degrees=True)

Auch hier ist das Objekt repräsentationsunabhängig und kann in jedes andere Format konvertiert werden

>>> r.as_quat()
array([0.        , 0.        , 0.70710678, 0.70710678])
>>> r.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> r.as_rotvec()
array([0.        , 0.        , 1.57079633])

Es ist auch möglich, mehrere Rotationen in einer einzigen Instanz mithilfe einer der from_...-Funktionen zu initialisieren. Hier initialisieren wir einen Stapel von 3 Rotationen mithilfe der from_euler-Methode

>>> r = R.from_euler('zyx', [
... [90, 0, 0],
... [0, 45, 0],
... [45, 60, 30]], degrees=True)

Die anderen Darstellungen geben nun ebenfalls einen Stapel von 3 Rotationen zurück. Zum Beispiel

>>> r.as_quat()
array([[0.        , 0.        , 0.70710678, 0.70710678],
       [0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])

Anwenden der obigen Rotationen auf einen Vektor

>>> v = [1, 2, 3]
>>> r.apply(v)
array([[-2.        ,  1.        ,  3.        ],
       [ 2.82842712,  2.        ,  1.41421356],
       [ 2.24452282,  0.78093109,  2.89002836]])

Eine Rotation-Instanz kann indiziert und gesliced werden, als wäre sie ein einzelnes 1D-Array oder eine Liste

>>> r.as_quat()
array([[0.        , 0.        , 0.70710678, 0.70710678],
       [0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])
>>> p = r[0]
>>> p.as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])
>>> q = r[1:3]
>>> q.as_quat()
array([[0.        , 0.38268343, 0.        , 0.92387953],
       [0.39190384, 0.36042341, 0.43967974, 0.72331741]])

Tatsächlich kann sie in ein numpy.array konvertiert werden

>>> r_array = np.asarray(r)
>>> r_array.shape
(3,)
>>> r_array[0].as_matrix()
array([[ 2.22044605e-16, -1.00000000e+00,  0.00000000e+00],
       [ 1.00000000e+00,  2.22044605e-16,  0.00000000e+00],
       [ 0.00000000e+00,  0.00000000e+00,  1.00000000e+00]])

Mehrere Rotationen können mithilfe des Operators * komponiert werden

>>> r1 = R.from_euler('z', 90, degrees=True)
>>> r2 = R.from_rotvec([np.pi/4, 0, 0])
>>> v = [1, 2, 3]
>>> r2.apply(r1.apply(v))
array([-2.        , -1.41421356,  2.82842712])
>>> r3 = r2 * r1 # Note the order
>>> r3.apply(v)
array([-2.        , -1.41421356,  2.82842712])

Eine Rotation kann mit sich selbst mithilfe des Operators ** komponiert werden

>>> p = R.from_rotvec([1, 0, 0])
>>> q = p ** 2
>>> q.as_rotvec()
array([2., 0., 0.])

Schließlich ist es auch möglich, Rotationen zu invertieren

>>> r1 = R.from_euler('z', [90, 45], degrees=True)
>>> r2 = r1.inv()
>>> r2.as_euler('zyx', degrees=True)
array([[-90.,   0.,   0.],
       [-45.,   0.,   0.]])

Die folgende Funktion kann verwendet werden, um Rotationen mit Matplotlib zu plotten, indem gezeigt wird, wie sie die Standard-x-, y-, z-Koordinatenachsen transformieren

>>> import matplotlib.pyplot as plt

>>> def plot_rotated_axes(ax, r, name=None, offset=(0, 0, 0), scale=1):
...     colors = ("#FF6666", "#005533", "#1199EE")  # Colorblind-safe RGB
...     loc = np.array([offset, offset])
...     for i, (axis, c) in enumerate(zip((ax.xaxis, ax.yaxis, ax.zaxis),
...                                       colors)):
...         axlabel = axis.axis_name
...         axis.set_label_text(axlabel)
...         axis.label.set_color(c)
...         axis.line.set_color(c)
...         axis.set_tick_params(colors=c)
...         line = np.zeros((2, 3))
...         line[1, i] = scale
...         line_rot = r.apply(line)
...         line_plot = line_rot + loc
...         ax.plot(line_plot[:, 0], line_plot[:, 1], line_plot[:, 2], c)
...         text_loc = line[1]*1.2
...         text_loc_rot = r.apply(text_loc)
...         text_plot = text_loc_rot + loc[0]
...         ax.text(*text_plot, axlabel.upper(), color=c,
...                 va="center", ha="center")
...     ax.text(*offset, name, color="k", va="center", ha="center",
...             bbox={"fc": "w", "alpha": 0.8, "boxstyle": "circle"})

Erstellen Sie drei Rotationen – die Identität und zwei Euler-Rotationen unter Verwendung intrinsischer und extrinsischer Konventionen

>>> r0 = R.identity()
>>> r1 = R.from_euler("ZYX", [90, -30, 0], degrees=True)  # intrinsic
>>> r2 = R.from_euler("zyx", [90, -30, 0], degrees=True)  # extrinsic

Fügen Sie alle drei Rotationen zu einem einzigen Plot hinzu

>>> ax = plt.figure().add_subplot(projection="3d", proj_type="ortho")
>>> plot_rotated_axes(ax, r0, name="r0", offset=(0, 0, 0))
>>> plot_rotated_axes(ax, r1, name="r1", offset=(3, 0, 0))
>>> plot_rotated_axes(ax, r2, name="r2", offset=(6, 0, 0))
>>> _ = ax.annotate(
...     "r0: Identity Rotation\n"
...     "r1: Intrinsic Euler Rotation (ZYX)\n"
...     "r2: Extrinsic Euler Rotation (zyx)",
...     xy=(0.6, 0.7), xycoords="axes fraction", ha="left"
... )
>>> ax.set(xlim=(-1.25, 7.25), ylim=(-1.25, 1.25), zlim=(-1.25, 1.25))
>>> ax.set(xticks=range(-1, 8), yticks=[-1, 0, 1], zticks=[-1, 0, 1])
>>> ax.set_aspect("equal", adjustable="box")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.tight_layout()

Zeigen Sie den Plot

>>> plt.show()

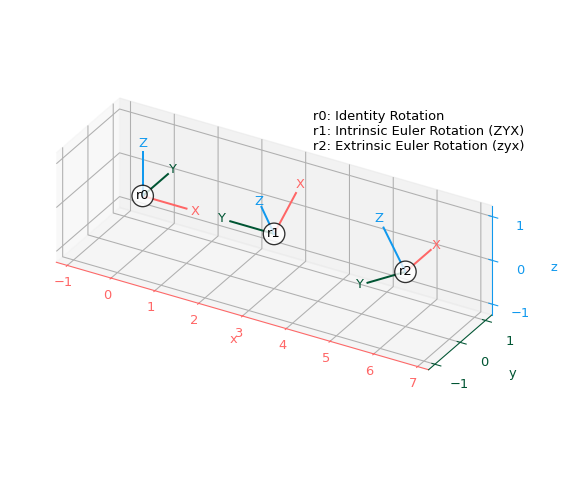
../../_images/scipy-spatial-transform-Rotation-1_00_00.png

Diese Beispiele dienen als Überblick über die Rotation-Klasse und heben die wichtigsten Funktionalitäten hervor. Für umfassendere Beispiele für die unterstützten Ein- und Ausgabeformate konsultieren Sie die Beispiele der einzelnen Methoden.