Pearson-Korrelation#
Betrachten Sie die folgenden Daten aus [1], die die Beziehung zwischen freiem Prolin (einer Aminosäure) und Gesamtcollagen (einem Protein, das häufig in Bindegewebe vorkommt) in ungesunden menschlichen Lebern untersuchten.
Die unten aufgeführten Arrays x und y erfassen Messungen der beiden Verbindungen. Die Beobachtungen sind gepaart: Jede Messung des freien Prolins wurde aus derselben Leber wie die Messung des Gesamt kollagens am selben Index entnommen.
import numpy as np
# total collagen (mg/g dry weight of liver)
x = np.array([7.1, 7.1, 7.2, 8.3, 9.4, 10.5, 11.4])
# free proline (μ mole/g dry weight of liver)
y = np.array([2.8, 2.9, 2.8, 2.6, 3.5, 4.6, 5.0])
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8, 5))
ax.plot(x, y, '.')
ax.set_xlabel("total collagen (mg/g)")
ax.set_ylabel("free proline (μ mole/g)")
plt.show()
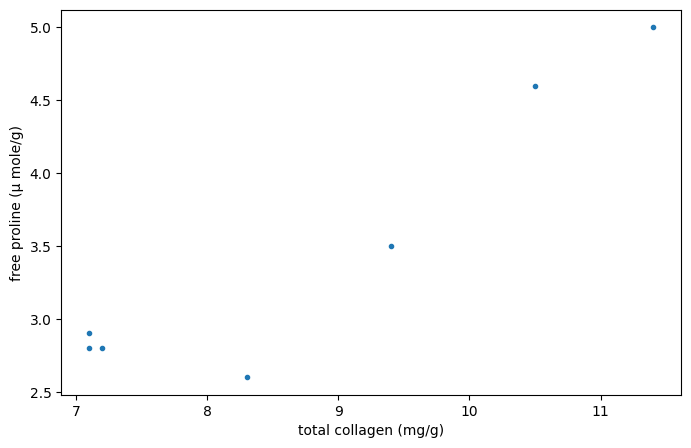
Diese Daten wurden in [2] mit dem Spearman-Korrelationskoeffizienten analysiert, einer Statistik, die für monotone Korrelationen zwischen den Stichproben empfindlich ist. Hier analysieren wir die Daten mit dem Pearson-Korrelationskoeffizienten ({class}scipy.stats.pearsonr`), der für lineare Korrelationen empfindlich ist.
from scipy import stats
res = stats.pearsonr(x, y)
res.statistic
np.float64(0.9347467974524514)
Der Wert dieser Statistik ist tendenziell hoch (nahe 1) für Stichproben mit einer stark positiven linearen Korrelation, niedrig (nahe -1) für Stichproben mit einer stark negativen linearen Korrelation und gering in der Magnitude (nahe null) für Stichproben mit schwacher linearer Korrelation.
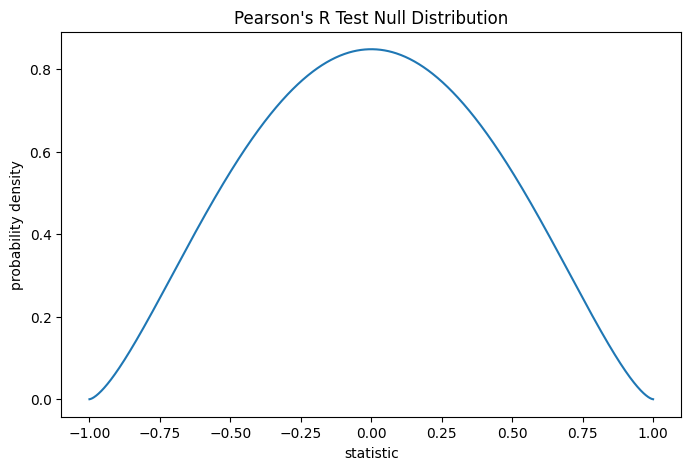
Der Test wird durchgeführt, indem der beobachtete Wert der Statistik mit der Nullverteilung verglichen wird: der Verteilung von Statistikwerten, die unter der Nullhypothese abgeleitet wurden, dass Gesamtcollagen- und freie Prolinmessungen aus unabhängigen Normalverteilungen stammen.
Unter der Nullhypothese ist der Populationskorrelationskoeffizient null, und der Stichprobenkorrelationskoeffizient folgt der Beta-Verteilung auf dem Intervall \((-1, 1)\) mit den Formparametern \(a = b = \frac{n}{2}-1\), wobei \(n\) die Anzahl der Beobachtungen in jeder Stichprobe ist.
n = len(x) # len(x) == len(y)
a = b = n/2 - 1 # shape parameter
loc, scale = -1, 2 # support is (-1, 1)
dist = stats.beta(a=a, b=b, loc=loc, scale=scale)
r_vals = np.linspace(-1, 1, 1000)
pdf = dist.pdf(r_vals)
fig, ax = plt.subplots(figsize=(8, 5))
def plot(ax): # we'll re-use this
ax.plot(r_vals, pdf)
ax.set_title("Pearson's R Test Null Distribution")
ax.set_xlabel("statistic")
ax.set_ylabel("probability density")
plot(ax)
plt.show()
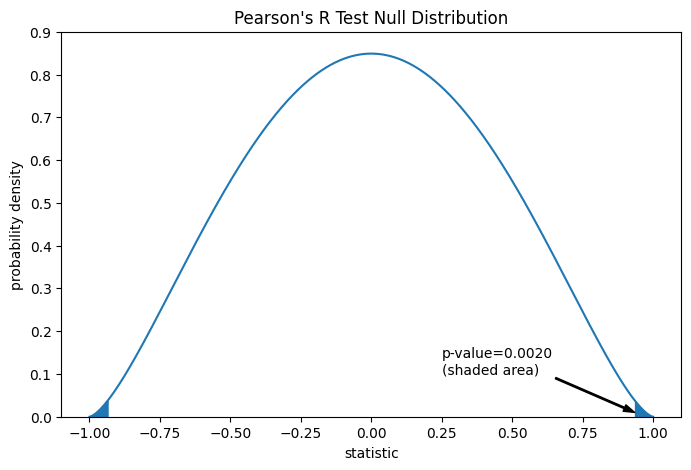
Der Vergleich wird durch den p-Wert quantifiziert: dem Anteil der Werte in der Nullverteilung, die so extrem oder extremer sind als der beobachtete Wert der Statistik. Bei einem zweiseitigen Test, bei dem die Statistik positiv ist, werden sowohl die Elemente der Nullverteilung, die größer als die transformierte Statistik sind, als auch die Elemente der Nullverteilung, die kleiner als das Negative des beobachteten Statistikwerts sind, als "extremer" betrachtet.
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
rs = res.statistic # original statistic
pvalue = dist.cdf(-rs) + dist.sf(rs)
annotation = (f'p-value={pvalue:.4f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (rs, 0.01), (0.25, 0.1), arrowprops=props)
i = r_vals >= rs
ax.fill_between(r_vals[i], y1=0, y2=pdf[i], color='C0')
i = r_vals <= -rs
ax.fill_between(r_vals[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(-1.1, 1.1)
ax.set_ylim(0, 0.9)
plt.show()
res.pvalue # two-sided p-value
np.float64(0.002016532795489407)
Wenn der p-Wert "klein" ist - das heißt, wenn die Wahrscheinlichkeit gering ist, Daten aus unabhängigen Normalverteilungen zu ziehen, die einen solch extremen Wert der Statistik ergeben -, kann dies als Beweis gegen die Nullhypothese zugunsten der Alternative genommen werden: Die Verteilung von Gesamtcollagen und freiem Prolin sind nicht unabhängig. Beachten Sie, dass
Das Umgekehrte gilt nicht; d.h. der Test wird nicht verwendet, um Beweise für die Nullhypothese zu liefern.
Der Schwellenwert für Werte, die als "klein" gelten, ist eine Wahl, die getroffen werden sollte, bevor die Daten analysiert werden [3], wobei die Risiken von sowohl falsch positiven Ergebnissen (fälschliches Ablehnen der Nullhypothese) als auch falsch negativen Ergebnissen (Nichtablehnen einer falschen Nullhypothese) berücksichtigt werden.
Kleine p-Werte sind kein Beweis für einen großen Effekt; vielmehr können sie nur einen Beweis für einen "signifikanten" Effekt liefern, was bedeutet, dass sie unter der Nullhypothese unwahrscheinlich aufgetreten wären.
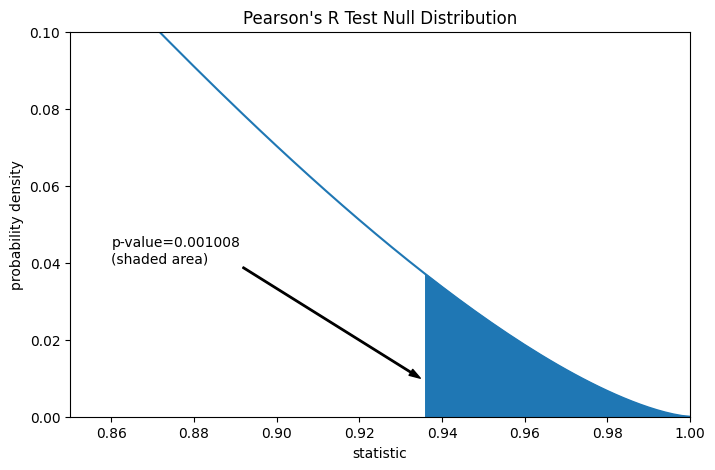
Angenommen, die Autoren hätten vor der Durchführung des Experiments Grund zu der Annahme einer positiven linearen Korrelation zwischen den Gesamtcollagen- und den freien Prolinmessungen gehabt und hätten sich entschieden, die Plausibilität der Nullhypothese gegenüber einer einseitigen Alternative zu bewerten: Freies Prolin hat eine positive lineare Korrelation mit Gesamtcollagen. In diesem Fall würden nur die Werte in der Nullverteilung, die gleich oder größer als die beobachtete Statistik sind, als extremer betrachtet werden.
res = stats.pearsonr(x, y, alternative='greater')
res.statistic
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
pvalue = dist.sf(rs)
annotation = (f'p-value={pvalue:.6f}\n(shaded area)')
props = dict(facecolor='black', width=1, headwidth=5, headlength=8)
_ = ax.annotate(annotation, (rs, 0.01), (0.86, 0.04), arrowprops=props)
i = r_vals >= rs
ax.fill_between(r_vals[i], y1=0, y2=pdf[i], color='C0')
ax.set_xlim(0.85, 1)
ax.set_ylim(0, 0.1)
plt.show()
res.pvalue # one-sided p-value; half of the two-sided p-value
np.float64(0.0010082663977447036)
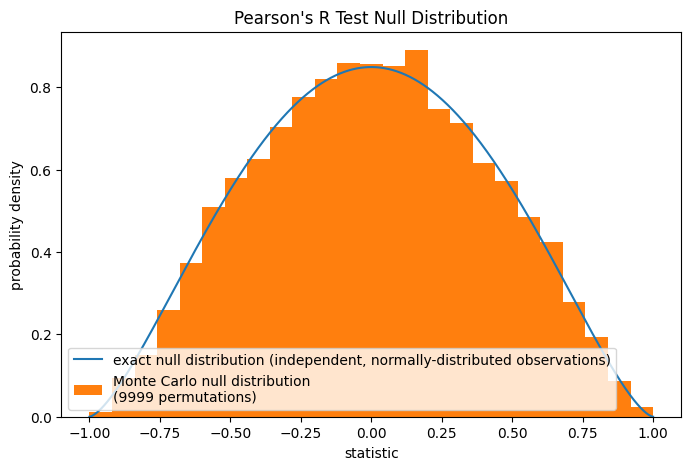
Beachten Sie, dass die Beta-Verteilung die exakte Nullverteilung für Stichproben jeder Größe unter dieser Nullhypothese ist. Wir können dies überprüfen, indem wir eine Monte-Carlo-Nullverteilung berechnen: explizit Stichproben aus unabhängigen Normalverteilungen ziehen und für jedes Paar die Pearson-Statistik berechnen.
rng = np.random.default_rng(332520619051409741187796892627751113442)
def statistic(x, y, axis):
return stats.pearsonr(x, y, axis=axis).statistic # ignore pvalue
ref = stats.monte_carlo_test((x, y), rvs=(rng.standard_normal, rng.standard_normal),
statistic=statistic, alternative='greater', n_resamples=9999)
fig, ax = plt.subplots(figsize=(8, 5))
plot(ax)
ax.hist(ref.null_distribution, np.linspace(-1, 1, 26), density=True)
ax.legend(['exact null distribution (independent, normally-distributed observations)',
f'Monte Carlo null distribution \n({len(ref.null_distribution)} permutations)'])
plt.show()
Dies ist oft eine angemessene Nullhypothese zum Testen, aber in anderen Fällen kann es geeigneter sein, einen Permutationstest durchzuführen: Unter der Nullhypothese, dass Gesamtcollagen und freies Prolin unabhängig sind (aber nicht unbedingt normalverteilt), ist jede der freien Prolinmessungen gleich wahrscheinlich mit jeder der Gesamtcollagenmessungen beobachtet zu werden. Daher können wir eine exakte Nullverteilung bilden, indem wir die Statistik unter jeder möglichen Paarung von Elementen zwischen x und y berechnen. Dies ist die Nullverteilung, die verwendet wird, wenn wir pearsonr mit method=stats.PermutationMethod() übergeben.
res = stats.pearsonr(x, y, alternative='greater', method=stats.PermutationMethod())
res.pvalue
np.float64(0.005555555555555556)