Kernel-Dichteschätzung

Eine häufige Aufgabe in der Statistik ist die Schätzung der Wahrscheinlichkeitsdichtefunktion (PDF) einer Zufallsvariablen aus einer Reihe von Datenstichproben. Diese Aufgabe wird als Dichteschätzung bezeichnet. Das bekannteste Werkzeug hierfür ist das Histogramm. Ein Histogramm ist ein nützliches Werkzeug zur Visualisierung (hauptsächlich, weil es jeder versteht), nutzt die verfügbaren Daten jedoch nicht sehr effizient. Die Kernel-Dichteschätzung (KDE) ist ein effizienteres Werkzeug für dieselbe Aufgabe. Der scipy.stats.gaussian_kde-Schätzer kann zur Schätzung der PDF von univariaten sowie multivariaten Daten verwendet werden. Er funktioniert am besten, wenn die Daten unimodal sind.

Univariate Schätzung

Wir beginnen mit einer minimalen Datenmenge, um zu sehen, wie scipy.stats.gaussian_kde funktioniert und welche unterschiedlichen Optionen für die Bandbreitenauswahl bewirken. Die aus der PDF gezogenen Daten werden als blaue Striche am unteren Rand der Abbildung dargestellt (dies wird als Rug Plot bezeichnet).

>>> import numpy as np
>>> from scipy import stats
>>> import matplotlib.pyplot as plt

>>> x1 = np.array([-7, -5, 1, 4, 5], dtype=np.float64)
>>> kde1 = stats.gaussian_kde(x1)
>>> kde2 = stats.gaussian_kde(x1, bw_method='silverman')

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)

>>> ax.plot(x1, np.zeros(x1.shape), 'b+', ms=20)  # rug plot
>>> x_eval = np.linspace(-10, 10, num=200)
>>> ax.plot(x_eval, kde1(x_eval), 'k-', label="Scott's Rule")
>>> ax.plot(x_eval, kde2(x_eval), 'r-', label="Silverman's Rule")

>>> plt.show()

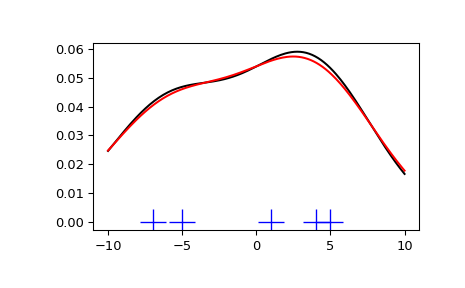
Wir sehen, dass es sehr geringe Unterschiede zwischen der Scott-Regel und der Silverman-Regel gibt und dass die Bandbreitenauswahl bei einer begrenzten Datenmenge wahrscheinlich etwas zu breit ist. Wir können unsere eigene Bandbreitenfunktion definieren, um ein weniger geglättetes Ergebnis zu erzielen.

>>> def my_kde_bandwidth(obj, fac=1./5):
...     """We use Scott's Rule, multiplied by a constant factor."""
...     return np.power(obj.n, -1./(obj.d+4)) * fac

>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)

>>> ax.plot(x1, np.zeros(x1.shape), 'b+', ms=20)  # rug plot
>>> kde3 = stats.gaussian_kde(x1, bw_method=my_kde_bandwidth)
>>> ax.plot(x_eval, kde3(x_eval), 'g-', label="With smaller BW")

>>> plt.show()

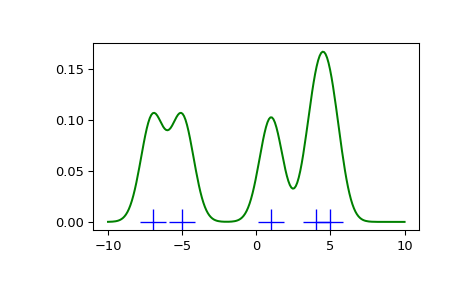
Wir sehen, dass, wenn wir die Bandbreite sehr schmal einstellen, die erhaltene Schätzung der Wahrscheinlichkeitsdichtefunktion (PDF) einfach die Summe von Gaußfunktionen um jeden Datenpunkt ist.

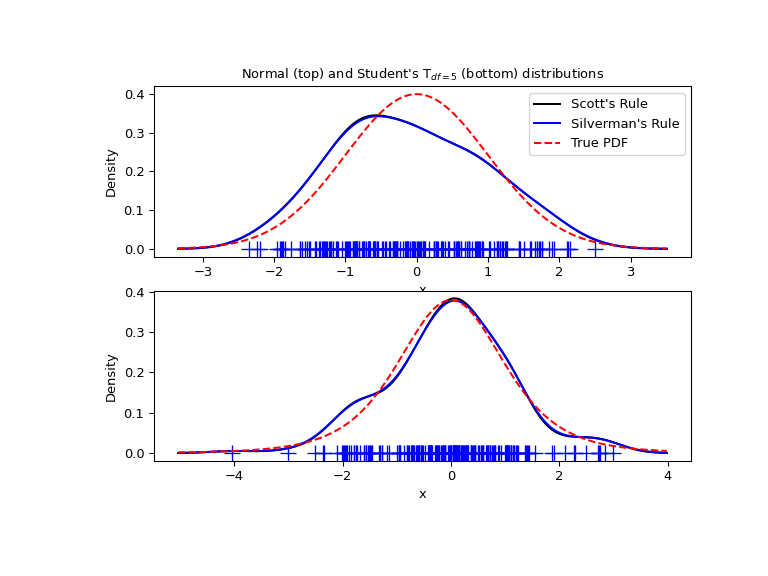
Wir nehmen nun ein realistischeres Beispiel und betrachten den Unterschied zwischen den beiden verfügbaren Regeln für die Bandbreitenauswahl. Diese Regeln funktionieren bekanntermaßen gut für (nahezu) normale Verteilungen, aber auch für unimodale Verteilungen, die ziemlich stark nicht-normal sind, funktionieren sie vernünftig gut. Als nicht-normale Verteilung nehmen wir eine Student’sche t-Verteilung mit 5 Freiheitsgraden.

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats


rng = np.random.default_rng()
x1 = rng.normal(size=200)  # random data, normal distribution
xs = np.linspace(x1.min()-1, x1.max()+1, 200)

kde1 = stats.gaussian_kde(x1)
kde2 = stats.gaussian_kde(x1, bw_method='silverman')

fig = plt.figure(figsize=(8, 6))

ax1 = fig.add_subplot(211)
ax1.plot(x1, np.zeros(x1.shape), 'b+', ms=12)  # rug plot
ax1.plot(xs, kde1(xs), 'k-', label="Scott's Rule")
ax1.plot(xs, kde2(xs), 'b-', label="Silverman's Rule")
ax1.plot(xs, stats.norm.pdf(xs), 'r--', label="True PDF")

ax1.set_xlabel('x')
ax1.set_ylabel('Density')
ax1.set_title("Normal (top) and Student's T$_{df=5}$ (bottom) distributions")
ax1.legend(loc=1)

x2 = stats.t.rvs(5, size=200, random_state=rng)  # random data, T distribution
xs = np.linspace(x2.min() - 1, x2.max() + 1, 200)

kde3 = stats.gaussian_kde(x2)
kde4 = stats.gaussian_kde(x2, bw_method='silverman')

ax2 = fig.add_subplot(212)
ax2.plot(x2, np.zeros(x2.shape), 'b+', ms=12)  # rug plot
ax2.plot(xs, kde3(xs), 'k-', label="Scott's Rule")
ax2.plot(xs, kde4(xs), 'b-', label="Silverman's Rule")
ax2.plot(xs, stats.t.pdf(xs, 5), 'r--', label="True PDF")

ax2.set_xlabel('x')
ax2.set_ylabel('Density')

plt.show()

Nun betrachten wir eine bimodale Verteilung mit einem breiteren und einem schmaleren Gaußschen Merkmal. Wir erwarten, dass dies eine schwierigere Dichte zur Annäherung sein wird, aufgrund der unterschiedlichen Bandbreiten, die erforderlich sind, um jedes Merkmal genau aufzulösen.

>>> from functools import partial

>>> loc1, scale1, size1 = (-2, 1, 175)
>>> loc2, scale2, size2 = (2, 0.2, 50)
>>> x2 = np.concatenate([np.random.normal(loc=loc1, scale=scale1, size=size1),
...                      np.random.normal(loc=loc2, scale=scale2, size=size2)])

>>> x_eval = np.linspace(x2.min() - 1, x2.max() + 1, 500)

>>> kde = stats.gaussian_kde(x2)
>>> kde2 = stats.gaussian_kde(x2, bw_method='silverman')
>>> kde3 = stats.gaussian_kde(x2, bw_method=partial(my_kde_bandwidth, fac=0.2))
>>> kde4 = stats.gaussian_kde(x2, bw_method=partial(my_kde_bandwidth, fac=0.5))

>>> pdf = stats.norm.pdf
>>> bimodal_pdf = pdf(x_eval, loc=loc1, scale=scale1) * float(size1) / x2.size + \
...               pdf(x_eval, loc=loc2, scale=scale2) * float(size2) / x2.size

>>> fig = plt.figure(figsize=(8, 6))
>>> ax = fig.add_subplot(111)

>>> ax.plot(x2, np.zeros(x2.shape), 'b+', ms=12)
>>> ax.plot(x_eval, kde(x_eval), 'k-', label="Scott's Rule")
>>> ax.plot(x_eval, kde2(x_eval), 'b-', label="Silverman's Rule")
>>> ax.plot(x_eval, kde3(x_eval), 'g-', label="Scott * 0.2")
>>> ax.plot(x_eval, kde4(x_eval), 'c-', label="Scott * 0.5")
>>> ax.plot(x_eval, bimodal_pdf, 'r--', label="Actual PDF")

>>> ax.set_xlim([x_eval.min(), x_eval.max()])
>>> ax.legend(loc=2)
>>> ax.set_xlabel('x')
>>> ax.set_ylabel('Density')
>>> plt.show()

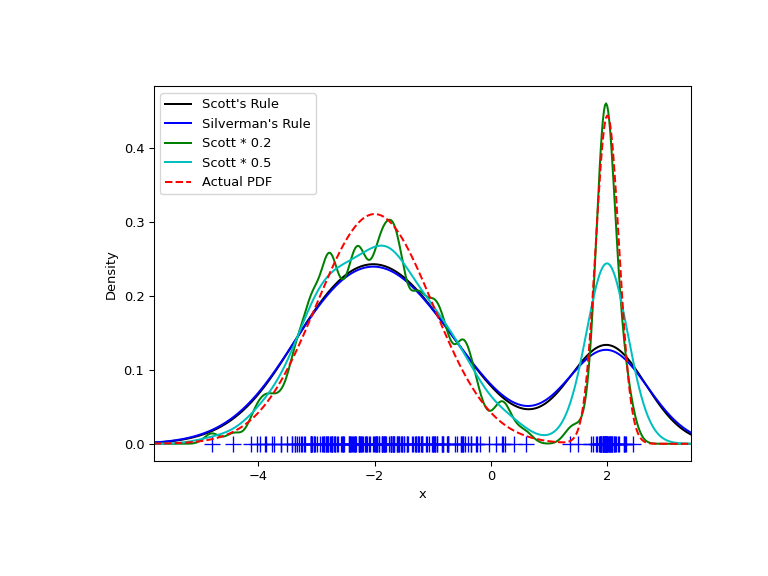
Wie erwartet, ist die KDE aufgrund der unterschiedlichen charakteristischen Größe der beiden Merkmale der bimodalen Verteilung nicht so nah an der wahren PDF, wie wir es uns wünschen würden. Durch Halbierung der Standardbandbreite (Scott * 0.5) können wir etwas bessere Ergebnisse erzielen, während eine um den Faktor 5 kleinere Bandbreite als die Standardbandbreite nicht genug Glättung bietet. Was wir in diesem Fall jedoch wirklich benötigen, ist eine nicht-uniforme (adaptive) Bandbreite.

Multivariate Schätzung

Mit scipy.stats.gaussian_kde können wir multivariate sowie univariate Schätzungen durchführen. Wir demonstrieren den bivariaten Fall. Zuerst generieren wir einige Zufallsdaten mit einem Modell, bei dem die beiden Variablen korreliert sind.

>>> def measure(n):
...     """Measurement model, return two coupled measurements."""
...     m1 = np.random.normal(size=n)
...     m2 = np.random.normal(scale=0.5, size=n)
...     return m1+m2, m1-m2

>>> m1, m2 = measure(2000)
>>> xmin = m1.min()
>>> xmax = m1.max()
>>> ymin = m2.min()
>>> ymax = m2.max()

Dann wenden wir die KDE auf die Daten an.

>>> X, Y = np.mgrid[xmin:xmax:100j, ymin:ymax:100j]
>>> positions = np.vstack([X.ravel(), Y.ravel()])
>>> values = np.vstack([m1, m2])
>>> kernel = stats.gaussian_kde(values)
>>> Z = np.reshape(kernel.evaluate(positions).T, X.shape)

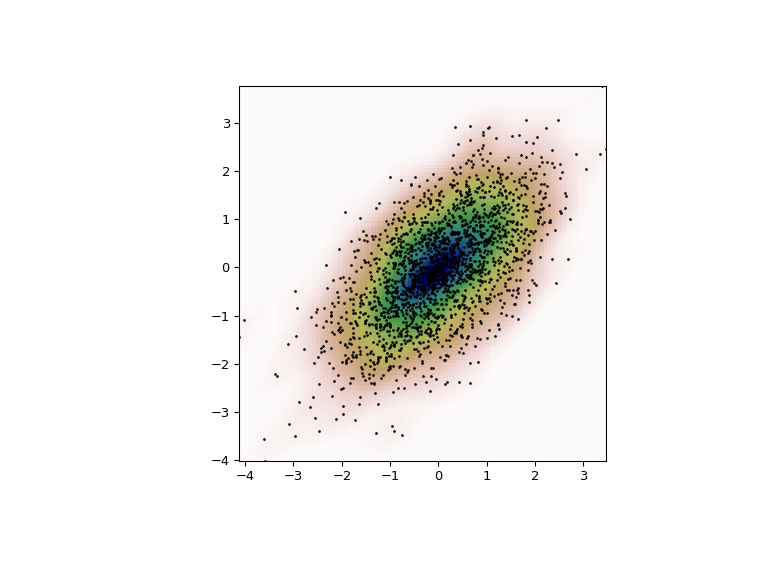
Schließlich plotten wir die geschätzte bivariate Verteilung als Farbleiste und legen die einzelnen Datenpunkte darüber.

>>> fig = plt.figure(figsize=(8, 6))
>>> ax = fig.add_subplot(111)

>>> ax.imshow(np.rot90(Z), cmap=plt.cm.gist_earth_r,
...           extent=[xmin, xmax, ymin, ymax])
>>> ax.plot(m1, m2, 'k.', markersize=2)

>>> ax.set_xlim([xmin, xmax])
>>> ax.set_ylim([ymin, ymax])

>>> plt.show()