Hermite-Interpolationsbasierte INVersion der CDF (HINV)#
Erforderlich: CDF
Optional: PDF, dPDF
Geschwindigkeit
Einrichtung: (sehr) langsam
Sampling: (sehr) schnell
HINV ist eine Variante der numerischen Inversion, bei der die inverse CDF mittels Hermite-Interpolation angenähert wird, d.h. das Intervall [0,1] wird in mehrere Intervalle unterteilt und in jedem Intervall wird die inverse CDF durch Polynome approximiert, die mittels Werten der CDF und PDF an den Intervallgrenzen konstruiert werden. Dies ermöglicht eine Verbesserung der Genauigkeit durch Unterteilung eines bestimmten Intervalls ohne Neuberechnungen in nicht betroffenen Intervallen. Drei Arten von Splines sind implementiert: lineare, kubische und quintische Interpolation. Für die lineare Interpolation wird nur die CDF benötigt. Die kubische Interpolation benötigt zusätzlich die PDF und die quintische Interpolation die PDF und ihre Ableitung.
Diese Splines müssen in einem Einrichtungsschritt berechnet werden. Sie funktioniert jedoch nur für Verteilungen mit beschränktem Definitionsbereich; für Verteilungen mit unbeschränktem Definitionsbereich werden die Enden abgeschnitten, so dass die Wahrscheinlichkeit für die Endbereiche im Vergleich zur gegebenen u-Auflösung gering ist.
Die Methode ist nicht exakt, da sie nur Zufallsvariablen der approximierten Verteilung erzeugt. Dennoch kann der maximale numerische Fehler in "u-Richtung" (d.h. |U - CDF(X)| wobei X das ungefähre Perzentil ist, das dem Quantil U entspricht, d.h. X = approx_ppf(U)) auf die erforderliche Auflösung (innerhalb der Maschinengenauigkeit) eingestellt werden. Beachten Sie, dass sehr kleine Werte der u-Auflösung möglich sind, aber die Kosten für den Einrichtungsschritt erhöhen können.
NumericalInverseHermite approximiert die Umkehrung der CDF einer kontinuierlichen statistischen Verteilung mit einem Hermite-Spline. Die Ordnung des Hermite-Splines kann durch Übergabe des Parameters order angegeben werden.
Wie in [1] beschrieben, beginnt sie mit der Auswertung der PDF und CDF der Verteilung an einem Gitter von Quantilen x innerhalb des Trägers der Verteilung. Sie verwendet die Ergebnisse, um einen Hermite-Spline H anzupassen, so dass H(p) == x, wobei p das Array der Perzentile ist, die den Quantilen x entsprechen. Daher approximiert der Spline die Umkehrung der CDF der Verteilung bis zur Maschinengenauigkeit bei den Perzentilen p, aber typischerweise wird der Spline nicht so genau in den Mittelpunkten zwischen den Perzentilpunkten sein.
p_mid = (p[:-1] + p[1:])/2
Daher wird das Gitter von Quantilen nach Bedarf verfeinert, um den maximalen "u-Fehler" zu reduzieren.
u_error = np.max(np.abs(dist.cdf(H(p_mid)) - p_mid))
unterhalb der angegebenen Toleranz u_resolution. Die Verfeinerung stoppt, wenn die erforderliche Toleranz erreicht ist oder wenn die Anzahl der Gitterintervalle nach der nächsten Verfeinerung die maximal zulässige Anzahl von Intervallen (100000) überschreiten könnte.
>>> import numpy as np
>>> from scipy.stats.sampling import NumericalInverseHermite
>>> from scipy.stats import norm, genexpon
>>> from scipy.special import ndtr
Um einen Generator zur Stichprobenentnahme aus der Standardnormalverteilung zu erstellen, tun Sie Folgendes:
>>> class StandardNormal:
... def pdf(self, x):
... return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
... def cdf(self, x):
... return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, random_state=urng)
Die NumericalInverseHermite verfügt über eine Methode zur Approximation der PPF der Verteilung.
>>> rng = NumericalInverseHermite(dist)
>>> p = np.linspace(0.01, 0.99, 99) # percentiles from 1% to 99%
>>> np.allclose(rng.ppf(p), norm.ppf(p))
True
Abhängig von der Implementierung der Zufallsstichprobenmethode der Verteilung können die generierten Zufallsvariablen bei gleichem Zufallszustand nahezu identisch sein.
>>> dist = genexpon(9, 16, 3)
>>> rng = NumericalInverseHermite(dist)
>>> # `seed` ensures identical random streams are used by each `rvs` method
>>> seed = 500072020
>>> rvs1 = dist.rvs(size=100, random_state=np.random.default_rng(seed))
>>> rvs2 = rng.rvs(size=100, random_state=np.random.default_rng(seed))
>>> np.allclose(rvs1, rvs2)
True
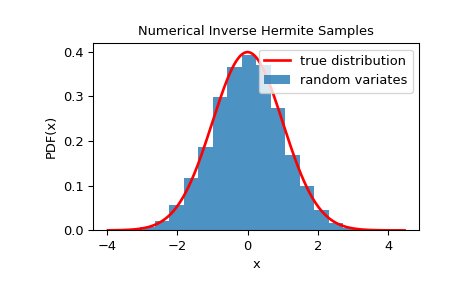
Um zu überprüfen, ob die Zufallsvariablen der gegebenen Verteilung eng folgen, können wir uns ihr Histogramm ansehen.
>>> import matplotlib.pyplot as plt
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, random_state=urng)
>>> rvs = rng.rvs(10000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Numerical Inverse Hermite Samples')
>>> plt.legend()
>>> plt.show()
Unter Angabe der Ableitung der PDF in Bezug auf die Zufallsvariable (d.h. x) können wir die quintische Hermite-Interpolation verwenden, um die PPF durch Übergabe des Parameters order zu approximieren.
>>> class StandardNormal:
... def pdf(self, x):
... return 1/np.sqrt(2*np.pi) * np.exp(-x**2 / 2)
... def dpdf(self, x):
... return -1/np.sqrt(2*np.pi) * x * np.exp(-x**2 / 2)
... def cdf(self, x):
... return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInverseHermite(dist, order=5, random_state=urng)
Höhere Ordnungen führen zu einer geringeren Anzahl von Intervallen.
>>> rng3 = NumericalInverseHermite(dist, order=3)
>>> rng5 = NumericalInverseHermite(dist, order=5)
>>> rng3.intervals, rng5.intervals
(3000, 522)
Der u-Fehler kann durch Aufruf der Methode u_error geschätzt werden. Sie führt eine kleine Monte-Carlo-Simulation durch, um den u-Fehler zu schätzen. Standardmäßig werden 100.000 Stichproben verwendet. Dies kann durch Übergabe des Arguments sample_size geändert werden.
>>> rng1 = NumericalInverseHermite(dist, u_resolution=1e-10)
>>> rng1.u_error(sample_size=1000000) # uses one million samples
UError(max_error=9.53167544892608e-11, mean_absolute_error=2.2450136432146864e-11)
Dies gibt ein benanntes Tupel zurück, das den maximalen u-Fehler und den mittleren absoluten u-Fehler enthält.
Der u-Fehler kann durch Verringern der u-Auflösung (maximal zulässiger u-Fehler) reduziert werden.
>>> rng2 = NumericalInverseHermite(dist, u_resolution=1e-13)
>>> rng2.u_error(sample_size=1000000)
UError(max_error=9.32027892364129e-14, mean_absolute_error=1.5194172675685075e-14)
Beachten Sie, dass dies auf Kosten der Rechenzeit geht, da die Einrichtung und die Anzahl der Intervalle zunehmen.
>>> rng1.intervals
1022
>>> rng2.intervals
5687
>>> from timeit import timeit
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-10)
>>> timeit(f, number=1)
0.017409582000254886 # may vary
>>> f = lambda: NumericalInverseHermite(dist, u_resolution=1e-13)
>>> timeit(f, number=1)
0.08671202100003939 # may vary
Weitere Details zu dieser Methode finden Sie in [1] und [2].