Glättende Splines#
Spline-Glättung in 1D#
Beim Interpolationsproblem besteht die Aufgabe darin, eine Kurve zu konstruieren, die durch eine gegebene Menge von Datenpunkten verläuft. Dies ist möglicherweise nicht angemessen, wenn die Daten verrauscht sind: Wir möchten dann eine glatte Kurve, \(g(x)\), konstruieren, die die Eingabedaten *annähert*, ohne jeden Punkt exakt zu durchlaufen.
Zu diesem Zweck ermöglicht scipy.interpolate die Konstruktion von *glättenden Splines*, die abwägen, wie nah die resultierende Kurve, \(g(x)\), an den Daten liegt und wie glatt \(g(x)\) ist. Mathematisch besteht die Aufgabe darin, ein gestraftes Kleinstquadrate-Problem zu lösen, wobei die Strafe die Glattheit von \(g(x)\) steuert.
Wir bieten zwei Ansätze zur Konstruktion von glättenden Splines an, die sich in (1) der Form des Strafterms und (2) der Basis, in der die glättende Kurve konstruiert wird, unterscheiden. Nachfolgend betrachten wir diese beiden Ansätze.
Die erstgenannte Variante wird von der Funktion make_smoothing_spline durchgeführt, einer Clean-Room-Neuentwicklung des klassischen Fortran-Pakets gcvspl von H. Woltring. Die letztgenannte Variante wird von der Funktion make_splrep implementiert, die eine Neuentwicklung der Fortran-Bibliothek FITPACK von P. Dierckx ist. Eine Legacy-Schnittstelle zur FITPACK-Bibliothek ist ebenfalls verfügbar.
„Klassische“ glättende Splines und das Kriterium der verallgemeinerten Kreuzvalidierung (GCV)#
Gegeben seien die Datenarrays x und y sowie das Array nicht-negativer *Gewichte*, w. Wir suchen eine kubische Spline-Funktion g(x), die minimiert
wobei \(\lambda \geqslant 0\) ein nicht-negativer Strahlparameter ist und \(g^{(2)}(x)\) die zweite Ableitung von \(g(x)\) ist. Die Summation im ersten Term läuft über die Datenpunkte, \((x_j, y_j)\), und das Integral im zweiten Term erstreckt sich über das gesamte Intervall \(x \in [x_1, x_n]\).
Hier bestraft der erste Term die Abweichung der Spline-Funktion von den Daten, und der zweite Term bestraft große Werte der zweiten Ableitung – was als Kriterium für die Glattheit einer Kurve angesehen wird.
Die Zielfunktion, \(g(x)\), wird als natürliche kubische Spline *mit Knoten an den Datenpunkten*, \(x_j\), angenommen, und die Minimierung wird über die Spline-Koeffizienten bei einem gegebenen Wert von \(\lambda\) durchgeführt.
Offensichtlich entspricht \(\lambda = 0\) dem Interpolationsproblem – das Ergebnis ist eine *natürliche interpolierende Spline*; im entgegengesetzten Grenzfall, \(\lambda \gg 1\), nähert sich das Ergebnis \(g(x)\) einer Geraden an (da die Minimierung effektiv die zweite Ableitung von \(g(x)\) nullt).
Die glättende Funktion hängt stark von \(\lambda\) ab, und es gibt mehrere Strategien zur Auswahl eines „optimalen“ Wertes der Strafe. Eine beliebte Strategie ist die sogenannte *verallgemeinerte Kreuzvalidierung* (GCV): Konzeptionell ist dies äquivalent zum Vergleich der Spline-Funktionen, die auf reduzierten Datensätzen konstruiert werden, bei denen ein Datenpunkt weggelassen wird. Die direkte Anwendung dieses Leave-One-Out-Kreuzvalidierungsverfahrens ist sehr aufwendig, und wir verwenden einen effizienteren GCV-Algorithmus.
Zur Konstruktion der glättenden Spline bei gegebenen Daten und dem Strahlparameter verwenden wir die Funktion make_smoothing_spline. Ihre Schnittstelle ähnelt dem Konstruktor für interpolierende Splines, make_interp_spline: Sie akzeptiert Datenarrays und gibt eine aufrufbare BSpline-Instanz zurück.
Zusätzlich akzeptiert sie ein optionales Schlüsselwortargument lam, um den Strahlparameter \(\lambda\) anzugeben. Wenn es weggelassen oder auf None gesetzt wird, wird \(\lambda\) über das GCV-Verfahren berechnet.
Um den Effekt des Strahlparameters zu veranschaulichen, betrachten wir ein Spielbeispiel einer Sinuskurve mit etwas Rauschen
>>> import numpy as np
>>> from scipy.interpolate import make_smoothing_spline
Generieren einiger verrauschter Daten
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y = np.sin(x) + 0.4*rng.standard_normal(size=len(x))
Konstruktion und Plotten von glättenden Splines für eine Reihe von Werten des Strahlparameters
>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> for lam in [0, 0.02, 10, None]:
... spl = make_smoothing_spline(x, y, lam=lam)
... plt.plot(xnew, spl(xnew), '-.', label=fr'$\lambda=${lam}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()
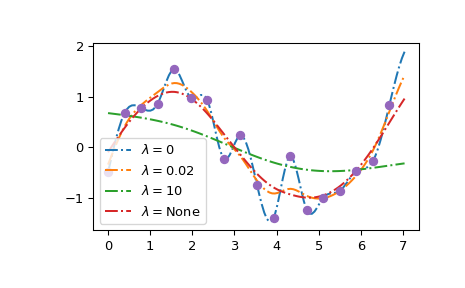
Wir sehen deutlich, dass lam=0 die interpolierende Spline konstruiert; große Werte von lam glätten die resultierende Kurve zu einer Geraden; und das GCV-Ergebnis, lam=None, liegt nahe an der zugrundeliegenden Sinuskurve.
Batch-Verarbeitung von y-Arrays#
make_smoothing_spline akzeptiert mehrdimensionale y-Arrays und einen optionalen axis-Parameter und interpretiert sie genau wie der Konstruktor für interpolierende Splines, make_interp_spline. Siehe den Abschnitt Interpolation für eine Diskussion und Beispiele.
Glättende Splines mit automatischer Knotenauswahl#
Als Ergänzung zu make_smoothing_spline bietet SciPy eine Alternative in Form der Routinen make_splrep und make_splprep. Die erstgenannte konstruiert Spline-Funktionen und die letztgenannte ist für parametrische Spline-Kurven in \(d > 1\) Dimensionen.
Während sie eine ähnliche API haben (Akzeptieren von Datenarrays, Rückgabe einer BSpline-Instanz), unterscheiden sie sich von make_smoothing_spline in mehrfacher Hinsicht:
die funktionale Form des Strafterms ist anders: diese Routinen verwenden *Sprünge* der \(k\)-ten Ableitung anstelle des Integrals der \((k-1)\)-ten Ableitung;
anstelle des Strahlparameters \(\lambda\) wird ein Glattheitsparameter \(s\) verwendet;
diese Routinen konstruieren den Knotenvektor automatisch; je nach Eingabe können resultierende Splines viel weniger Knoten als Datenpunkte haben.
standardmäßig unterscheiden sich die Randbedingungen: während
make_smoothing_splinenatürliche kubische Splines konstruiert, verwenden diese Routinen standardmäßig die Not-A-Knot-Randbedingungen.
Betrachten wir den Algorithmus detaillierter. Erstens, **das Glättungskriterium**. Gegeben eine kubische Spline-Funktion, \(g(x)\), definiert durch die Knoten, \(t_j\), und Koeffizienten, \(c_j\), betrachten wir die Sprünge der dritten Ableitung an den inneren Knoten,
(Für Splines vom Grad \(k\) hätten wir Sprünge der \(k\)-ten Ableitung verwendet.)
Wenn alle \(D_j = 0\) sind, dann ist \(g(x)\) ein einzelnes Polynom auf dem gesamten von den Knoten aufgespannten Bereich. Wir betrachten daher \(g(x)\) als eine stückweise \(C^2\)-differenzierbare Spline-Funktion und verwenden als Glättungskriterium die Summe der Sprünge,
wobei die durchgeführte Minimierung über die Spline-Koeffizienten und potenziell die Spline-Knoten erfolgt.
Um sicherzustellen, dass \(g(x)\) die Eingabedaten, \(x_j\) und \(y_j\), annähert, führen wir den *Glattheitsparameter* \(s \geqslant 0\) ein und fügen die Bedingung hinzu, dass
In dieser Formulierung ist der Glattheitsparameter \(s\) eine Benutzereingabe, ähnlich wie der Strahlparameter \(\lambda\) für klassische glättende Splines.
Beachten Sie, dass der Grenzwert s = 0 dem Interpolationsproblem entspricht, bei dem \(g(x_j) = y_j\) gilt. Ein Ansteigen von s führt zu glatteren Fits, und im Grenzwert eines sehr großen s degeneriert \(g(x)\) zu einem einzelnen besten Fit-Polynom.
Für einen festen Knotenvektor und einen gegebenen Wert von \(s\) ist das Minimierungsproblem linear. Wenn wir auch bezüglich der Knoten minimieren, wird das Problem nichtlinear. Wir müssen daher ein iteratives Minimierungsverfahren angeben, um *den Knotenvektor* zusammen mit den Spline-Koeffizienten zu *konstruieren*.
Wir verwenden daher das folgende Verfahren:
wir beginnen mit einer Spline ohne innere Knoten und überprüfen die Glattheitsbedingung für den vom Benutzer angegebenen Wert von \(s\). Wenn sie erfüllt ist, sind wir fertig. Andernfalls,
iterieren wir, wobei wir in jeder Iteration
neue Knoten hinzufügen, indem wir das Intervall mit der größten Abweichung zwischen der Spline-Funktion \(g(x_j)\) und den Daten \(y_j\) aufteilen.
die nächste Annäherung für \(g(x)\) konstruieren und das Glättungskriterium überprüfen.
Die Iterationen stoppen, entweder wenn die Glattheitsbedingung erfüllt ist oder wenn die maximal zulässige Anzahl von Knoten erreicht ist. Letzteres kann entweder vom Benutzer angegeben werden oder nimmt den Standardwert len(x) + k + 1 an, was der Interpolation des Datenarrays x mit Splines vom Grad k entspricht.
Umformuliert und Details weggelassen, besteht das Verfahren darin, über die von generate_knots generierten Knotenvektoren zu iterieren und bei jedem Schritt make_lsq_spline anzuwenden. In Pseudocode
for t in generate_knots(x, y, s=s):
g = make_lsq_spline(x, y, t=t) # construct
if ((y - g(x))**2).sum() < s: # check smoothness
break
Hinweis
Für s=0 machen wir eine Abkürzung und konstruieren die interpolierende Spline mit der Not-A-Knot-Randbedingung anstatt zu iterieren.
Das iterative Verfahren zur Konstruktion eines Knotenvektors ist über die Generatorfunktion generate_knots verfügbar. Zur Veranschaulichung
>>> import numpy as np
>>> from scipy.interpolate import generate_knots
>>> x = np.arange(7)
>>> y = x**4
>>> list(generate_knots(x, y, s=1)) # default is cubic splines, k=3
[array([0., 0., 0., 0., 6., 6., 6., 6.]),
array([0., 0., 0., 0., 3., 6., 6., 6., 6.]),
array([0., 0., 0., 0., 3., 5., 6., 6., 6., 6.]),
array([0., 0., 0., 0., 2., 3., 4., 6., 6., 6., 6.])]
Für s=0 kürzt der Generator ab
>>> list(generate_knots(x, y, s=0))
[array([0, 0, 0, 0, 2, 3, 4, 6, 6, 6, 6])]
Hinweis
Im Allgemeinen werden Knoten an Datenstellen platziert. Die Ausnahme bilden Splines geraden Grades, bei denen die Knoten von den Daten entfernt platziert werden können. Dies geschieht, wenn s=0 (Interpolation) ist oder wenn s klein genug ist, sodass die maximale Anzahl von Knoten erreicht wird und die Routine zum Knotenvektor für s=0 (auch bekannt als Greville-Abzisse) wechselt.
>>> list(generate_knots(x, y, s=1, k=2)) # k=2, quadratic spline
[array([0., 0., 0., 6., 6., 6.]),
array([0., 0., 0., 3., 6., 6., 6.]),
array([0., 0., 0., 3., 5., 6., 6., 6.]),
array([0., 0., 0., 2., 3., 5., 6., 6., 6.]),
array([0. , 0. , 0. , 1.5, 2.5, 3.5, 4.5, 6. , 6. , 6. ])] # Greville sites
Hinweis
Die Heuristiken für die Konstruktion des Knotenvektors folgen dem Algorithmus der FITPACK-Fortran-Bibliothek. Der Algorithmus ist derselbe, und kleine Unterschiede sind aufgrund von Gleitkomma-Rundungen möglich.
Wir veranschaulichen nun die Ergebnisse von make_splrep unter Verwendung desselben Spiel-Datensatzes wie im vorherigen Abschnitt
>>> import numpy as np
>>> from scipy.interpolate import make_splrep
Generieren einiger verrauschter Daten
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y = np.sin(x) + 0.4*rng.standard_normal(size=len(x))
Konstruktion und Plotten von glättenden Splines für eine Reihe von Werten des s-Parameters
>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, make_splrep(x, y, s=0)(xnew), '-', label='s=0')
>>> plt.plot(xnew, make_splrep(x, y, s=len(x))(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()
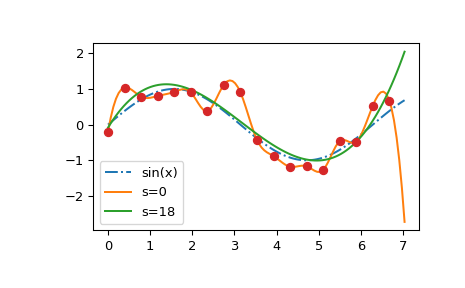
Wir sehen, dass die \(s=0\)-Kurve den (zufälligen) Schwankungen der Datenpunkte folgt, während die \(s > 0\)-Kurve nahe an der zugrundeliegenden Sinusfunktion liegt. Beachten Sie auch, dass die extrapolierten Werte je nach Wert von \(s\) stark schwanken.
Das Finden eines guten Wertes für \(s\) ist ein Versuch-und-Irrtum-Prozess. Wenn die Gewichte den Kehrwerten der Standardabweichungen der Eingabedaten entsprechen, wird ein „guter“ Wert von \(s\) voraussichtlich irgendwo zwischen \(m - \sqrt{2m}\) und \(m + \sqrt{2m}\) liegen, wobei \(m\) die Anzahl der Datenpunkte ist. Wenn alle Gewichte gleich eins sind, könnte eine vernünftige Wahl etwa \(s \sim m\,\sigma^2\) sein, wobei \(\sigma\) ein Schätzer für die Standardabweichung der Daten ist.
Hinweis
Die Anzahl der Knoten hängt sehr stark von s ab. Es ist möglich, dass kleine Variationen von s zu drastischen Änderungen der Knotenzahl führen.
Hinweis
Sowohl make_smoothing_spline als auch make_splrep erlauben gewichtete Fits, bei denen der Benutzer ein Array von Gewichten, w, bereitstellt. Beachten Sie, dass die Definition etwas abweicht: make_smoothing_spline quadriert die Gewichte, um mit gcvspl konsistent zu sein, während make_splrep dies nicht tut – um mit FITPACK konsistent zu sein.
Glättende Spline-Kurven in \(d>1\)#
Bisher betrachteten wir die Konstruktion von glättenden Spline-Funktionen, \(g(x)\), gegeben die Datenarrays x und y. Nun betrachten wir ein verwandtes Problem der Konstruktion einer glättenden Spline-*Kurve*, bei der wir die Daten als Punkte in einer Ebene, \(\mathbf{p}_j = (x_j, y_j)\), betrachten und eine parametrische Funktion \(\mathbf{g}(\mathbf{p}) = (g_x(u), g_y(u))\) konstruieren wollen, wobei die Werte des Parameters \(u_j\) \(x_j\) und \(y_j\) entsprechen.
Beachten Sie, dass sich dieses Problem leicht auf höhere Dimensionen, \(d > 2\), verallgemeinern lässt: Wir haben einfach \(d\) Datenarrays und konstruieren eine parametrische Funktion mit \(d\) Komponenten.
Beachten Sie auch, dass die Wahl der Parametrisierung nicht automatisiert werden kann und verschiedene Parametrisierungen zu sehr unterschiedlichen Kurven für dieselben Daten führen können, selbst für *interpolierende Kurven* (Interpolating Spline Curves).
Sobald eine bestimmte Form der Parametrisierung gewählt ist, ist das Problem der Konstruktion einer glättenden Kurve konzeptionell sehr ähnlich der Konstruktion einer glättenden Spline-Funktion. Kurz gesagt,
Spline-Knoten werden aus den Werten des Parameters \(u\) hinzugefügt, und
sowohl die zu minimierende Kostenfunktion als auch die Bedingung, die wir für Spline-Funktionen betrachtet haben, erhalten einfach eine zusätzliche Summation über die \(d\) Komponenten.
Die „parametrische“ Verallgemeinerung der Funktion make_splrep ist make_splprep, und ihr Docstring erläutert die genaue mathematische Formulierung des Minimierungsproblems, das sie löst.
Der wichtigste für den Benutzer sichtbare Unterschied des parametrischen Falls ist die Benutzeroberfläche:
anstelle von zwei Datenarrays,
xundy, erhältmake_splprepein einzelnes zweidimensionales Array, wobei die zweite Dimension die Größe \(d\) hat und jedes Datenarray entlang der ersten Dimension gespeichert ist (alternativ können Sie eine Liste von 1D-Arrays angeben).der Rückgabewert ist ein Paar: eine
BSpline-Instanz und das Array der Parameterwerte,u, das den Eingabedatenarrays entspricht.
Standardmäßig konstruiert und gibt make_splprep die Bogenlängenparametrisierung der Eingabedaten zurück (siehe den Abschnitt Parametrische Spline-Kurven für Details). Alternativ können Sie Ihr eigenes Array von Parameterwerten, u, angeben.
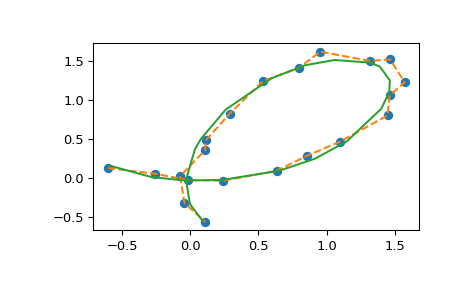
Zur Veranschaulichung der API betrachten wir ein Spielproblem: Wir haben einige Daten, die aus einer Descartes-Blume *plus* etwas Rauschen abgetastet wurden.
>>> import numpy as np
>>> from scipy.interpolate import make_splprep
>>> th = np.linspace(-0.2, np.pi/2 + 0.2, 21)
>>> r = 3 * np.sin(th) * np.cos(th) / (np.sin(th)**3 + np.cos(th)**3)
>>> x, y = r * np.cos(th), r * np.sin(th)
Rauschen hinzufügen und die Interpolatoren konstruieren
>>> rng = np.random.default_rng()
>>> xn = x + 0.1*rng.uniform(-1, 1, size=len(x))
>>> yn = y + 0.1*rng.uniform(-1, 1, size=len(x))
>>> spl, u = make_splprep([xn, yn], s=0) # note the [xn, yn] argument
>>> spl_n, u_n = make_splprep([xn, yn], s=0.1)
Und die Ergebnisse plotten (das Ergebnis von spl(u) ist ein 2D-Array, also packen wir es zum Plotten in ein Paar von x- und y-Arrays aus).
>>> import matplotlib.pyplot as plt
>>> plt.plot(xn, yn, 'o')
>>> plt.plot(*spl(u), '--')
>>> plt.plot(*spl_n(u_n), '-')
>>> plt.show()
Batch-Verarbeitung von y-Arrays#
Im Gegensatz zu *interpolierenden Splines* (Interpolating Splines) und *GCV-Glättern* (GCV Smoothers) erlauben make_splrep und make_splprep **nicht** mehrdimensionale y-Arrays und verlangen, dass x.ndim == y.ndim == 1.
Der technische Grund für diese Einschränkung ist, dass die Länge des Knotenvektors t von den y-Werten abhängt. Daher könnte für ein ge-batchtes y das ge-batchte t ein „ragged array“ sein, das BSpline nicht verarbeiten kann.
Daher müssen Sie, wenn Sie ge-batchte Eingaben verarbeiten müssen, über den Batch manuell iterieren und für jeden Slice des Batches ein BSpline-Objekt konstruieren. Nachdem Sie dies getan haben, können Sie das Verhalten von BSpline für Auswertungen mit einem Workaround wie folgt nachahmen
class BatchSpline:
"""BSpline-like class with batch behavior."""
def __init__(self, x, y, axis, *, spline, **kwargs):
y = np.moveaxis(y, axis, -1)
self._batch_shape = y.shape[:-1]
self._splines = [
spline(x, yi, **kwargs) for yi in y.reshape(-1, y.shape[-1])
]
self._axis = axis
def __call__(self, x):
y = [spline(x) for spline in self._splines]
y = np.reshape(y, self._batch_shape + x.shape)
return np.moveaxis(y, -1, self._axis) if x.shape else y
Legacy-Routinen für Spline-Glättung in 1D#
Zusätzlich zu den glättenden Spline-Konstruktoren, die wir in den vorherigen Abschnitten besprochen haben, bietet scipy.interpolate direkte Schnittstellen zu Routinen aus der ehrwürdigen FITPACK-Fortran-Bibliothek von P. Dierckx.
Hinweis
Diese Schnittstellen sollten als *Legacy* betrachtet werden – obwohl wir nicht vorhaben, sie zu veraltet zu erklären oder zu entfernen, empfehlen wir, dass neuer Code stattdessen modernere Alternativen wie make_smoothing_spline, make_splrep oder make_splprep verwendet.
Aus historischen Gründen bietet scipy.interpolate zwei äquivalente Schnittstellen für FITPACK: eine prozedurale Schnittstelle und eine objektorientierte Schnittstelle. Obwohl äquivalent, haben diese Schnittstellen unterschiedliche Standardwerte. Nachfolgend besprechen wir sie der Reihe nach, beginnend mit der prozeduralen Schnittstelle.
Prozedural (splrep)#
Spline-Interpolation erfordert zwei wesentliche Schritte: (1) eine Spline-Repräsentation der Kurve wird berechnet, und (2) die Spline wird an den gewünschten Punkten ausgewertet. Um die Spline-Repräsentation zu finden, gibt es zwei verschiedene Möglichkeiten, eine Kurve darzustellen und (glättende) Spline-Koeffizienten zu erhalten: direkt und parametrisch. Die direkte Methode findet die Spline-Repräsentation einer Kurve in einer 2D-Ebene unter Verwendung der Funktion splrep. Die ersten beiden Argumente sind die einzigen erforderlichen, und diese liefern die \(x\)- und \(y\)-Komponenten der Kurve. Die normale Ausgabe ist ein 3-Tupel, \(\left(t,c,k\right)\), das die Knotenpunkte, \(t\), die Koeffizienten \(c\) und den Grad \(k\) der Spline enthält. Der Standard-Spline-Grad ist kubisch, dies kann aber mit dem Eingabeschlüsselwort *k* geändert werden.
Das Knoten-Array definiert das Interpolationsintervall als t[k:-k], sodass die ersten \(k+1\) und die letzten \(k+1\) Einträge des t-Arrays *Randknoten* definieren. Die Koeffizienten sind ein 1D-Array von mindestens der Länge len(t) - k - 1. Einige Routinen füllen dieses Array auf, sodass len(c) == len(t) gilt – diese zusätzlichen Koeffizienten werden für die Spline-Auswertung ignoriert.
Das `tck`-Tupelformat ist mit interpolierenden B-Splines kompatibel: Die Ausgabe von `splrep` kann in ein `BSpline`-Objekt verpackt werden, z. B. `BSpline(*tck)`, und die unten beschriebenen Auswertungs-, Integrations- und Wurzelbehandlungsroutinen können `tck`-Tupel und `BSpline`-Objekte austauschbar verwenden.
Für Kurven im N-dimensionalen Raum ermöglicht die Funktion `splprep` die parametrische Definition der Kurve. Für diese Funktion wird nur 1 Eingabeargument benötigt. Diese Eingabe ist eine Liste von N Arrays, die die Kurve im N-dimensionalen Raum darstellen. Die Länge jedes Arrays ist die Anzahl der Kurvenpunkte, und jedes Array liefert eine Komponente des N-dimensionalen Datenpunkts. Die Parameter Variable wird mit dem Schlüsselwortargument `u` angegeben, das standardmäßig eine gleichmäßig verteilte monotone Sequenz zwischen 0 und 1 ist (d. h. die uniforme Parametrisierung).
Die Ausgabe besteht aus zwei Objekten: einem 3-Tupel, (t,c,k) , das die Spline-Darstellung und die Parameter Variable u enthält.
Die Koeffizienten sind eine Liste von N Arrays, wobei jedes Array einer Dimension der Eingabedaten entspricht. Beachten Sie, dass die Stützstellen, `t`, der Parametrisierung der Kurve `u` entsprechen.
Das Schlüsselwortargument `s` wird verwendet, um den Grad der Glättung während der Spline-Anpassung anzugeben. Der Standardwert von `s` ist `s=m-sqrt(2m)`, wobei `m` die Anzahl der angepassten Datenpunkte ist. Daher sollte, **wenn keine Glättung gewünscht ist, der Wert `s=0` an die Routinen übergeben werden.**
Sobald die Spline-Darstellung der Daten ermittelt wurde, kann sie entweder mit der Funktion `splev` ausgewertet oder das `tck`-Tupel wie unten gezeigt in ein `BSpline`-Objekt verpackt werden.
Wir beginnen damit, die Auswirkung des Parameters `s` auf die Glättung synthetischer verrauschter Daten zu veranschaulichen
>>> import numpy as np
>>> from scipy.interpolate import splrep, BSpline
Generieren einiger verrauschter Daten
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/16)
>>> rng = np.random.default_rng()
>>> y = np.sin(x) + 0.4*rng.standard_normal(size=len(x))
Konstruiere zwei Splines mit unterschiedlichen Werten für `s`.
>>> tck = splrep(x, y, s=0)
>>> tck_s = splrep(x, y, s=len(x))
Und plote sie
>>> import matplotlib.pyplot as plt
>>> xnew = np.arange(0, 9/4, 1/50) * np.pi
>>> plt.plot(xnew, np.sin(xnew), '-.', label='sin(x)')
>>> plt.plot(xnew, BSpline(*tck)(xnew), '-', label='s=0')
>>> plt.plot(xnew, BSpline(*tck_s)(xnew), '-', label=f's={len(x)}')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()
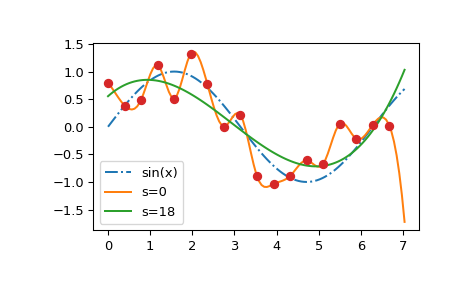
Wir sehen, dass die Kurve mit `s=0` den (zufälligen) Schwankungen der Datenpunkte folgt, während die Kurve mit `s > 0` nahe der zugrunde liegenden Sinusfunktion liegt. Beachten Sie auch, dass die extrapolierten Werte stark vom Wert von `s` abhängen.
Der Standardwert von `s` hängt davon ab, ob Gewichte angegeben werden oder nicht, und unterscheidet sich auch für `splrep` und `splprep`. Daher empfehlen wir, den Wert von `s` immer explizit anzugeben.
Manipulation von Spline-Objekten: prozedural (`splXXX`)#
Sobald die Spline-Darstellung der Daten ermittelt wurde, stehen Funktionen zur Auswertung der Spline (`splev`) und ihrer Ableitungen (`splev`, `spalde`) an beliebigen Punkten sowie das Integral der Spline zwischen zwei beliebigen Punkten (`splint`) zur Verfügung. Darüber hinaus können für kubische Splines (k=3) mit 8 oder mehr Stützstellen die Wurzeln der Spline geschätzt werden (`sproot`). Diese Funktionen werden im folgenden Beispiel demonstriert.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate
Kubische Spline
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = interpolate.splev(xnew, tck, der=0)
Beachten Sie, dass die letzte Zeile äquivalent zu `BSpline(*tck)(xnew)` ist.
>>> plt.figure()
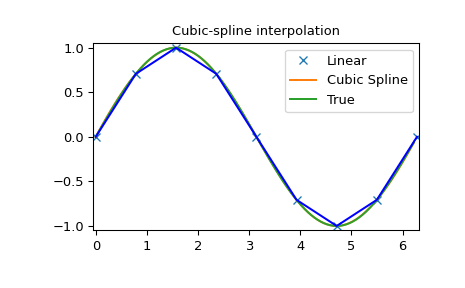
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Cubic-spline interpolation')
>>> plt.show()
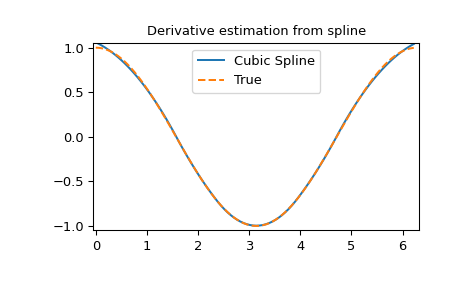
Ableitung der Spline
>>> yder = interpolate.splev(xnew, tck, der=1) # or BSpline(*tck)(xnew, 1)
>>> plt.figure()
>>> plt.plot(xnew, yder, xnew, np.cos(xnew),'--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Derivative estimation from spline')
>>> plt.show()
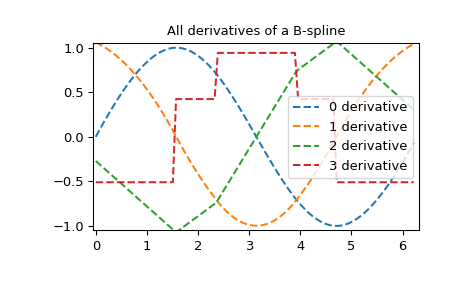
Alle Ableitungen der Spline
>>> yders = interpolate.spalde(xnew, tck)
>>> plt.figure()
>>> for i in range(len(yders[0])):
... plt.plot(xnew, [d[i] for d in yders], '--', label=f"{i} derivative")
>>> plt.legend()
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('All derivatives of a B-spline')
>>> plt.show()
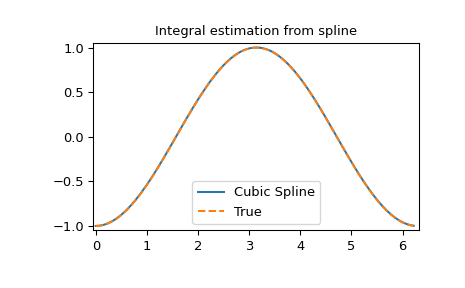
Integral der Spline
>>> def integ(x, tck, constant=-1):
... x = np.atleast_1d(x)
... out = np.zeros(x.shape, dtype=x.dtype)
... for n in range(len(out)):
... out[n] = interpolate.splint(0, x[n], tck)
... out += constant
... return out
>>> yint = integ(xnew, tck)
>>> plt.figure()
>>> plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
>>> plt.legend(['Cubic Spline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Integral estimation from spline')
>>> plt.show()
Wurzeln der Spline
>>> interpolate.sproot(tck)
array([3.1416]) # may vary
Beachten Sie, dass `sproot` möglicherweise keine offensichtliche Lösung am Rand des Approximationsintervalls, `x = 0`, findet. Wenn wir die Spline auf einem leicht größeren Intervall definieren, erhalten wir beide Wurzeln `x = 0` und `x = pi`.
>>> x = np.linspace(-np.pi/4, np.pi + np.pi/4, 51)
>>> y = np.sin(x)
>>> tck = interpolate.splrep(x, y, s=0)
>>> interpolate.sproot(tck)
array([0., 3.1416])
Parametrische Spline
>>> t = np.arange(0, 1.1, .1)
>>> x = np.sin(2*np.pi*t)
>>> y = np.cos(2*np.pi*t)
>>> tck, u = interpolate.splprep([x, y], s=0)
>>> unew = np.arange(0, 1.01, 0.01)
>>> out = interpolate.splev(unew, tck)
>>> plt.figure()
>>> plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
>>> plt.legend(['Linear', 'Cubic Spline', 'True'])
>>> plt.axis([-1.05, 1.05, -1.05, 1.05])
>>> plt.title('Spline of parametrically-defined curve')
>>> plt.show()
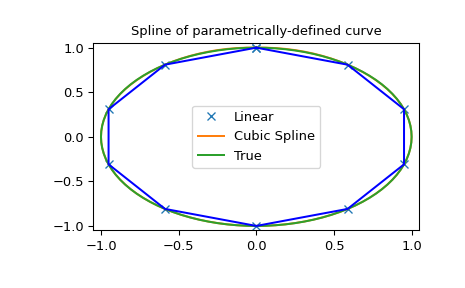
Beachten Sie, dass im letzten Beispiel `splprep` die Spline-Koeffizienten als Liste von Arrays zurückgibt, wobei jedes Array einer Dimension der Eingabedaten entspricht. Um die Ausgabe in eine `BSpline` zu verpacken, müssen wir daher die Koeffizienten transponieren (oder `BSpline(..., axis=1)` verwenden).
>>> tt, cc, k = tck
>>> cc = np.array(cc)
>>> bspl = BSpline(tt, cc.T, k) # note the transpose
>>> xy = bspl(u)
>>> xx, yy = xy.T # transpose to unpack into a pair of arrays
>>> np.allclose(x, xx)
True
>>> np.allclose(y, yy)
True
Objektorientiert (`UnivariateSpline`)#
Die oben beschriebenen Spline-Anpassungsfähigkeiten sind auch über eine objektorientierte Schnittstelle verfügbar. Die 1D-Splines sind Objekte der Klasse `UnivariateSpline` und werden mit den x- und y-Komponenten der als Argumente an den Konstruktor übergebenen Kurve erstellt. Die Klasse definiert `__call__`, wodurch das Objekt mit den x-Achsenwerten aufgerufen werden kann, an denen die Spline ausgewertet werden soll, und die interpolierten y-Werte zurückgegeben werden. Dies wird im folgenden Beispiel für die Unterklasse `InterpolatedUnivariateSpline` gezeigt. Die Methoden `integral`, `derivatives` und `roots` sind ebenfalls für `UnivariateSpline`-Objekte verfügbar und ermöglichen die Berechnung von bestimmten Integralen, Ableitungen und Wurzeln für die Spline.
Die Klasse `UnivariateSpline` kann auch zur Glättung von Daten verwendet werden, indem ein von Null verschiedener Wert des Glättungsparameters `s` angegeben wird, mit der gleichen Bedeutung wie der `s`-Schlüssel von der Funktion `splrep` oben. Dies ergibt eine Spline, die weniger Stützstellen als die Anzahl der Datenpunkte hat und daher keine strikt interpolierende Spline mehr ist, sondern eher eine glättende Spline. Wenn dies nicht gewünscht ist, ist die Klasse `InterpolatedUnivariateSpline` verfügbar. Sie ist eine Unterklasse von `UnivariateSpline`, die immer durch alle Punkte verläuft (entspricht dem Erzwingen des Glättungsparameters auf 0). Diese Klasse wird im folgenden Beispiel demonstriert.
Die Klasse `LSQUnivariateSpline` ist die andere Unterklasse von `UnivariateSpline`. Sie ermöglicht dem Benutzer, die Anzahl und Position der inneren Stützstellen explizit mit dem Parameter `t` anzugeben. Dies ermöglicht die Erstellung benutzerdefinierter Splines mit nicht-linearer Verteilung, um in einigen Domänen zu interpolieren und in anderen zu glätten oder den Charakter der Spline zu ändern.
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import interpolate
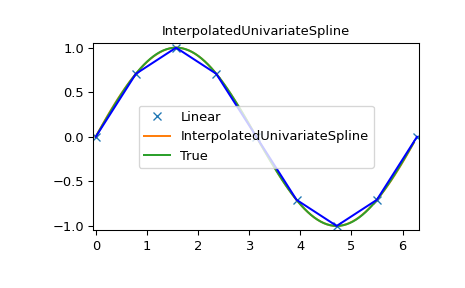
InterpolatedUnivariateSpline
>>> x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
>>> y = np.sin(x)
>>> s = interpolate.InterpolatedUnivariateSpline(x, y)
>>> xnew = np.arange(0, 2*np.pi, np.pi/50)
>>> ynew = s(xnew)
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'InterpolatedUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('InterpolatedUnivariateSpline')
>>> plt.show()
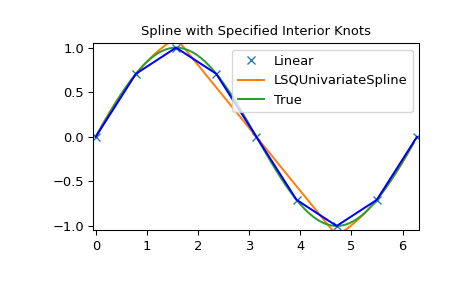
LSQUnivarateSpline mit nicht-uniformen Stützstellen
>>> t = [np.pi/2-.1, np.pi/2+.1, 3*np.pi/2-.1, 3*np.pi/2+.1]
>>> s = interpolate.LSQUnivariateSpline(x, y, t, k=2)
>>> ynew = s(xnew)
>>> plt.figure()
>>> plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
>>> plt.legend(['Linear', 'LSQUnivariateSpline', 'True'])
>>> plt.axis([-0.05, 6.33, -1.05, 1.05])
>>> plt.title('Spline with Specified Interior Knots')
>>> plt.show()
2D-Glättungs-Splines#
Zusätzlich zur Glättung von 1D-Splines bietet die FITPACK-Bibliothek die Mittel zur Anpassung von 2D-Oberflächen an zweidimensionale Daten. Die Oberflächen können als Funktionen von zwei Argumenten, `z = g(x, y)`, betrachtet werden, die als Tensorprodukte von 1D-Splines konstruiert sind.
Unter der Annahme, dass die Daten in drei Arrays, `x`, `y` und `z`, gespeichert sind, gibt es zwei Möglichkeiten, wie diese Datenarrays interpretiert werden können. Erstens - das interpolationsproblem mit gestreuten Daten - die Daten werden als gepaart angenommen, d.h. die Wertepaare `x[i]` und `y[i]` repräsentieren die Koordinaten des Punktes `i`, der `z[i]` entspricht.
Die Oberfläche `g(x, y)` wird so konstruiert, dass sie gilt
wobei `w_i` nicht-negative Gewichte sind und `s` der Eingabeparameter ist, bekannt als Glättungsfaktor, der das Zusammenspiel zwischen der Glattheit der resultierenden Funktion `g(x, y)` und der Qualität der Approximation der Daten (d. h. der Unterschiede zwischen `g(x_i, y_i)` und `z_i`) steuert. Der Grenzwert von `s = 0` entspricht formal der Interpolation, bei der die Oberfläche durch die Eingabedaten verläuft, `g(x_i, y_i) = z_i`. Siehe jedoch die Anmerkung unten.
Der zweite Fall - das interpolationsproblem auf einem rechteckigen Gitter - ist, bei dem die Datenpunkte auf einem rechteckigen Gitter angenommen werden, das durch alle Paare der Elemente der Arrays `x` und `y` definiert ist. Für dieses Problem wird angenommen, dass das Array `z` zweidimensional ist und `z[i, j]` `(x[i], y[j])` entspricht. Die bivariate Spline-Funktion `g(x, y)` wird so konstruiert, dass sie gilt
wobei `s` der Glättungsfaktor ist. Hier entspricht auch der Grenzwert von `s=0` formal der Interpolation, `g(x_i, y_j) = z_{i, j}`.
Hinweis
Intern wird die glättende Oberfläche `g(x, y)` durch Platzieren von Spline-Stützstellen in die Begrenzungsbox, die durch die Datenarrays definiert ist, konstruiert. Die Stützstellen werden automatisch über den FITPACK-Algorithmus platziert, bis die gewünschte Glattheit erreicht ist.
Die Stützstellen können sich von den Datenpunkten entfernt befinden.
Während `s=0` formal einer bi-variaten Spline-Interpolation entspricht, ist der FITPACK-Algorithmus nicht für Interpolation gedacht und kann zu unerwarteten Ergebnissen führen.
Für die Interpolation von gestreuten Daten bevorzugen Sie `griddata`; für Daten auf einem regulären Gitter bevorzugen Sie `RegularGridInterpolator`.
Hinweis
Wenn die Eingabedaten, `x` und `y`, so beschaffen sind, dass die Eingabedimensionen inkommensurable Einheiten haben und sich um viele Größenordnungen unterscheiden, kann der Interpolant `g(x, y)` numerische Artefakte aufweisen. Erwägen Sie, die Daten vor der Interpolation zu skalieren.
Wir betrachten nun nacheinander die beiden Spline-Anpassungsprobleme.
Bivariate Spline-Anpassung von gestreuten Daten#
Es gibt zwei Schnittstellen für die zugrunde liegende FITPACK-Bibliothek, eine prozedurale und eine objektorientierte Schnittstelle.
Prozedurale Schnittstelle (`bisplrep`)
Für die (glatte) Spline-Anpassung an eine 2D-Oberfläche steht die Funktion `bisplrep` zur Verfügung. Diese Funktion nimmt als erforderliche Eingaben die **1D**-Arrays `x`, `y` und `z` entgegen, die Punkte auf der Oberfläche `z=f(x, y)` darstellen. Die Spline-Ordnungen in x- und y-Richtung können über die optionalen Parameter `kx` und `ky` angegeben werden. Standardmäßig handelt es sich um eine bikubische Spline, `kx=ky=3`.
Die Ausgabe von `bisplrep` ist eine Liste `[tx,ty, c, kx, ky]`, deren Einträge die Komponenten der Stützstellenpositionen, die Koeffizienten der Spline und die Ordnung der Spline in jeder Koordinate darstellen. Es ist praktisch, diese Liste in einem einzigen Objekt, `tck`, zu halten, damit sie leicht an die Funktion `bisplev` übergeben werden kann. Der Schlüsselwortparameter `s` kann verwendet werden, um die Stärke der Glättung der Daten während der Bestimmung der geeigneten Spline zu ändern. Die empfohlenen Werte für `s` hängen von den Gewichten `w_i` ab. Wenn diese als `1/d_i` angenommen werden, wobei `d_i` eine Schätzung der Standardabweichung von `z_i` ist, sollte ein guter Wert für `s` im Bereich `m-sqrt(2m), m + sqrt(2m)` liegen, wobei `m` die Anzahl der Datenpunkte in den Vektoren `x`, `y` und `z` ist.
Der Standardwert ist `s=m-sqrt(2m)`. Daher sollte, **wenn keine Glättung gewünscht ist, ``s=0`` an `bisplrep` übergeben werden**. (Siehe jedoch die Anmerkung oben).
Um die 2D-Spline und ihre partiellen Ableitungen (bis zur Ordnung der Spline) auszuwerten, ist die Funktion `bisplev` erforderlich. Diese Funktion nimmt als erste beiden Argumente **zwei 1D-Arrays** entgegen, deren Kreuzprodukt den Bereich definiert, über den die Spline ausgewertet werden soll. Das dritte Argument ist die `tck`-Liste, die von `bisplrep` zurückgegeben wird. Falls gewünscht, geben die vierte und fünfte Argumente die Ordnungen der partiellen Ableitung in x- und y-Richtung an.
Hinweis
Es ist wichtig zu beachten, dass die 2D-Interpolation nicht zur Ermittlung der Spline-Darstellung von Bildern verwendet werden sollte. Der verwendete Algorithmus ist für eine große Anzahl von Eingabepunkten nicht geeignet. `scipy.signal` und `scipy.ndimage` enthalten geeignetere Algorithmen zur Ermittlung der Spline-Darstellung eines Bildes.
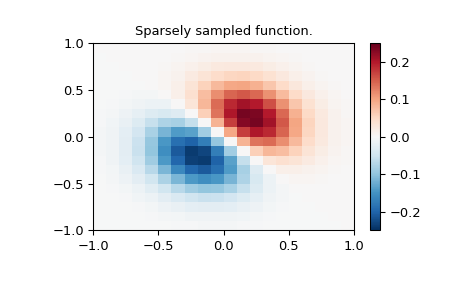
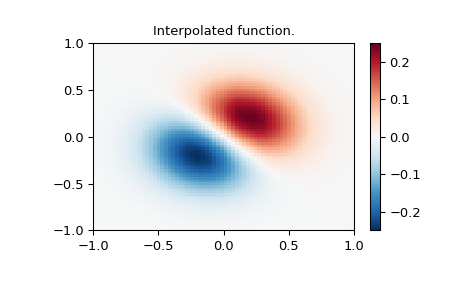
Die 2D-Interpolationsbefehle sind für die Verwendung bei der Interpolation einer 2D-Funktion wie im folgenden Beispiel vorgesehen. Dieses Beispiel verwendet den Befehl `mgrid` in NumPy, der nützlich ist, um ein "Mesh-Grid" in vielen Dimensionen zu definieren. (Siehe auch den Befehl `ogrid`, wenn das vollständige Mesh nicht benötigt wird). Die Anzahl der Ausgabeargumente und die Anzahl der Dimensionen jedes Arguments werden durch die Anzahl der Indizierungsobjekte bestimmt, die in `mgrid` übergeben werden.
>>> import numpy as np
>>> from scipy import interpolate
>>> import matplotlib.pyplot as plt
Funktion über ein spärliches 20x20-Gitter definieren
>>> x_edges, y_edges = np.mgrid[-1:1:21j, -1:1:21j]
>>> x = x_edges[:-1, :-1] + np.diff(x_edges[:2, 0])[0] / 2.
>>> y = y_edges[:-1, :-1] + np.diff(y_edges[0, :2])[0] / 2.
>>> z = (x+y) * np.exp(-6.0*(x*x+y*y))
>>> plt.figure()
>>> lims = dict(cmap='RdBu_r', vmin=-0.25, vmax=0.25)
>>> plt.pcolormesh(x_edges, y_edges, z, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Sparsely sampled function.")
>>> plt.show()
Funktion über ein neues 70x70-Gitter interpolieren
>>> xnew_edges, ynew_edges = np.mgrid[-1:1:71j, -1:1:71j]
>>> xnew = xnew_edges[:-1, :-1] + np.diff(xnew_edges[:2, 0])[0] / 2.
>>> ynew = ynew_edges[:-1, :-1] + np.diff(ynew_edges[0, :2])[0] / 2.
>>> tck = interpolate.bisplrep(x, y, z, s=0)
>>> znew = interpolate.bisplev(xnew[:,0], ynew[0,:], tck)
>>> plt.figure()
>>> plt.pcolormesh(xnew_edges, ynew_edges, znew, shading='flat', **lims)
>>> plt.colorbar()
>>> plt.title("Interpolated function.")
>>> plt.show()
Objektorientierte Schnittstelle (`SmoothBivariateSpline`)
Die objektorientierte Schnittstelle für die Glättung bi-variater Splines von gestreuten Daten, die Klasse `SmoothBivariateSpline`, implementiert eine Teilmenge der Funktionalität des Paares `bisplrep` / `bisplev` und hat andere Standardwerte.
Sie nimmt die Elemente des Gewichtsarrays als Eins an, `w_i = 1`, und konstruiert die Stützstellenvektoren automatisch anhand des Eingabewerts des Glättungsfaktors `s` - der Standardwert ist `m`, die Anzahl der Datenpunkte.
Die Spline-Ordnungen in x- und y-Richtung werden durch die optionalen Parameter `kx` und `ky` gesteuert, mit dem Standardwert `kx=ky=3`.
Wir illustrieren die Auswirkung des Glättungsfaktors anhand des folgenden Beispiels
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import SmoothBivariateSpline
import warnings
warnings.simplefilter('ignore')
train_x, train_y = np.meshgrid(np.arange(-5, 5, 0.5), np.arange(-5, 5, 0.5))
train_x = train_x.flatten()
train_y = train_y.flatten()
def z_func(x, y):
return np.cos(x) + np.sin(y) ** 2 + 0.05 * x + 0.1 * y
train_z = z_func(train_x, train_y)
interp_func = SmoothBivariateSpline(train_x, train_y, train_z, s=0.0)
smth_func = SmoothBivariateSpline(train_x, train_y, train_z)
test_x = np.arange(-9, 9, 0.01)
test_y = np.arange(-9, 9, 0.01)
grid_x, grid_y = np.meshgrid(test_x, test_y)
interp_result = interp_func(test_x, test_y).T
smth_result = smth_func(test_x, test_y).T
perfect_result = z_func(grid_x, grid_y)
fig, axes = plt.subplots(1, 3, figsize=(16, 8))
extent = [test_x[0], test_x[-1], test_y[0], test_y[-1]]
opts = dict(aspect='equal', cmap='nipy_spectral', extent=extent, vmin=-1.5, vmax=2.5)
im = axes[0].imshow(perfect_result, **opts)
fig.colorbar(im, ax=axes[0], orientation='horizontal')
axes[0].plot(train_x, train_y, 'w.')
axes[0].set_title('Perfect result, sampled function', fontsize=21)
im = axes[1].imshow(smth_result, **opts)
axes[1].plot(train_x, train_y, 'w.')
fig.colorbar(im, ax=axes[1], orientation='horizontal')
axes[1].set_title('s=default', fontsize=21)
im = axes[2].imshow(interp_result, **opts)
fig.colorbar(im, ax=axes[2], orientation='horizontal')
axes[2].plot(train_x, train_y, 'w.')
axes[2].set_title('s=0', fontsize=21)
plt.tight_layout()
plt.show()
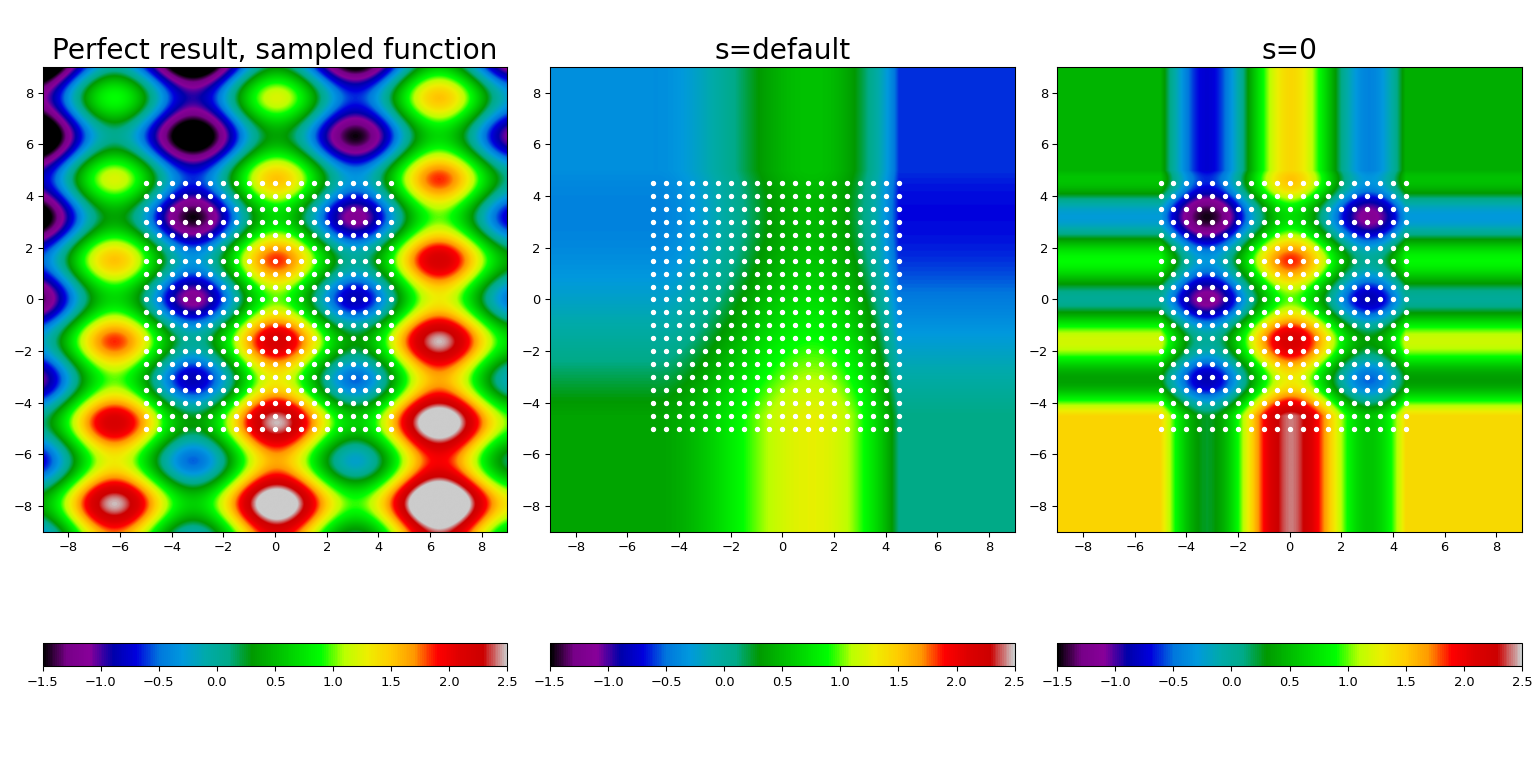
Hier nehmen wir eine bekannte Funktion (dargestellt im linken Feld), sampeln sie auf einem Punktgitter (gezeigt durch weiße Punkte) und konstruieren die Spline-Anpassung mit der Standardglättung (mittleres Feld) und indem wir die Interpolation erzwingen (rechtes Feld).
Mehrere Merkmale sind deutlich erkennbar. Erstens liefert der Standardwert von `s` zu viel Glättung für diese Daten; das Erzwingen der Interpolationsbedingung, `s = 0`, ermöglicht es, die zugrunde liegende Funktion mit angemessener Genauigkeit wiederherzustellen. Zweitens wird außerhalb des Interpolationsbereichs (d. h. des Bereichs, der von weißen Punkten abgedeckt wird) eine Extrapolation mit einer konstanten nächstgelegenen Nachbarmethode durchgeführt. Schließlich mussten wir die Warnungen unterdrücken (was schlechter Stil ist, ja!).
Die Warnung wird hier im Fall `s=0` ausgegeben und signalisiert eine interne Schwierigkeit, auf die FITPACK stieß, als wir die Interpolationsbedingung erzwangen. Wenn Sie diese Warnung in Ihrem Code sehen, sollten Sie erwägen, auf `bisplrep` umzusteigen und seine Parameter `nxest`, `nyest` zu erhöhen (siehe die Dokumentation von `bisplrep` für weitere Details).
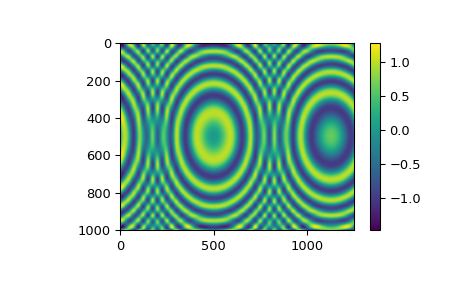
Bivariate Spline-Anpassung von Daten auf einem Gitter#
Für gegitterte 2D-Daten kann die Anpassung einer glättenden Tensorprodukt-Spline mit der Klasse `RectBivariateSpline` erfolgen. Sie hat eine ähnliche Schnittstelle wie `SmoothBivariateSpline`, wobei der Hauptunterschied darin besteht, dass die 1D-Eingabearrays `x` und `y` als Definition eines 2D-Gitters (als ihr äußeres Produkt) verstanden werden und das `z`-Array 2D mit der Form `len(x)` mal `len(y)` ist.
Die Spline-Ordnungen in x- und y-Richtung werden durch die optionalen Parameter `kx` und `ky` gesteuert, mit dem Standardwert `kx=ky=3`, d. h. eine bikubische Spline.
Der Standardwert des Glättungsfaktors ist `s=0`. Wir empfehlen dennoch, `s` immer explizit anzugeben.
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import RectBivariateSpline
x = np.arange(-5.01, 5.01, 0.25) # the grid is an outer product
y = np.arange(-5.01, 7.51, 0.25) # of x and y arrays
xx, yy = np.meshgrid(x, y, indexing='ij')
z = np.sin(xx**2 + 2.*yy**2) # z array needs to be 2-D
func = RectBivariateSpline(x, y, z, s=0)
xnew = np.arange(-5.01, 5.01, 1e-2)
ynew = np.arange(-5.01, 7.51, 1e-2)
znew = func(xnew, ynew)
plt.imshow(znew)
plt.colorbar()
plt.show()
Bivariate Spline-Anpassung von Daten in sphärischen Koordinaten#
Wenn Ihre Daten in sphärischen Koordinaten gegeben sind, `r = r(theta, phi)`, bieten `SmoothSphereBivariateSpline` und `RectSphereBivariateSpline` praktische Analoga zu `SmoothBivariateSpline` bzw. `RectBivariateSpline`.
Diese Klassen stellen die Periodizität der Spline-Anpassungen für `theta in [0, pi]` und `phi in [0, 2*pi]` sicher und bieten einige Kontrolle über die Kontinuität an den Polen. Einzelheiten finden Sie in den Dokumentationen dieser Klassen.