1-D Interpolation#

Stückweise lineare Interpolation#

Wenn Sie nur eine lineare (auch bekannt als Knicklinien-) Interpolation benötigen, können Sie die Funktion numpy.interp verwenden. Sie nimmt zwei Datenarrays zur Interpolation, x und y, und ein drittes Array, xnew, von Punkten, auf denen die Interpolation ausgewertet werden soll.

>>> import numpy as np
>>> x = np.linspace(0, 10, num=11)
>>> y = np.cos(-x**2 / 9.0)

Konstruktion der Interpolation

>>> xnew = np.linspace(0, 10, num=1001)
>>> ynew = np.interp(xnew, x, y)

Und plotten Sie es

>>> import matplotlib.pyplot as plt
>>> plt.plot(xnew, ynew, '-', label='linear interp')
>>> plt.plot(x, y, 'o', label='data')
>>> plt.legend(loc='best')
>>> plt.show()

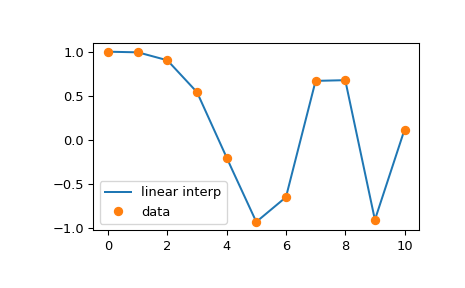
Eine Einschränkung von numpy.interp ist, dass sie keine Kontrolle über die Extrapolation erlaubt. Sehen Sie sich den Abschnitt Interpolation mit B-Splines für alternative Routinen an, die diese Art von Funktionalität bieten.

Kubische Splines#

Stückweise lineare Interpolation erzeugt natürlich Ecken an Datenpunkten, wo lineare Stücke zusammenstoßen. Um eine glattere Kurve zu erzeugen, können Sie kubische Splines verwenden, bei denen die interpolierende Kurve aus kubischen Stücken mit übereinstimmenden ersten und zweiten Ableitungen besteht. Im Code werden diese Objekte durch Instanzen der Klasse CubicSpline dargestellt. Eine Instanz wird mit den Datenarrays x und y konstruiert und kann dann mit den Zielwerten xnew ausgewertet werden.

>>> from scipy.interpolate import CubicSpline
>>> spl = CubicSpline([1, 2, 3, 4, 5, 6], [1, 4, 8, 16, 25, 36])
>>> spl(2.5)
5.57

Die Methode __call__ eines CubicSpline-Objekts akzeptiert sowohl Skalarwerte als auch Arrays. Sie akzeptiert auch ein zweites Argument, nu, um die Ableitung der Ordnung nu auszuwerten. Als Beispiel plotten wir die Ableitungen eines Splines.

>>> from scipy.interpolate import CubicSpline
>>> x = np.linspace(0, 10, num=11)
>>> y = np.cos(-x**2 / 9.)
>>> spl = CubicSpline(x, y)

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(4, 1, figsize=(5, 7))
>>> xnew = np.linspace(0, 10, num=1001)
>>> ax[0].plot(xnew, spl(xnew))
>>> ax[0].plot(x, y, 'o', label='data')
>>> ax[1].plot(xnew, spl(xnew, nu=1), '--', label='1st derivative')
>>> ax[2].plot(xnew, spl(xnew, nu=2), '--', label='2nd derivative')
>>> ax[3].plot(xnew, spl(xnew, nu=3), '--', label='3rd derivative')
>>> for j in range(4):
...     ax[j].legend(loc='best')
>>> plt.tight_layout()
>>> plt.show()

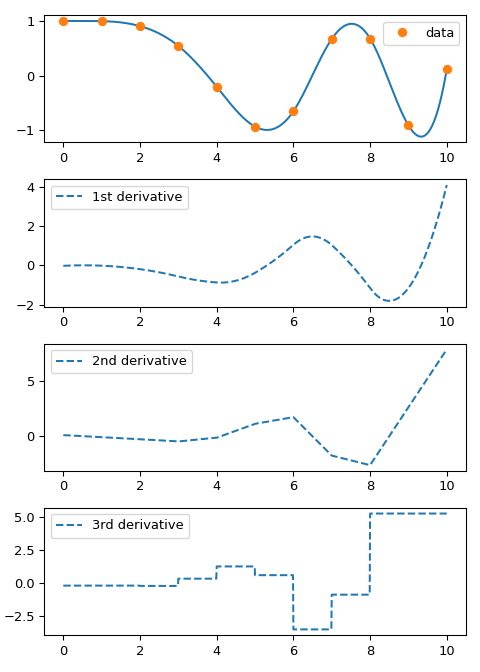
Beachten Sie, dass die erste und zweite Ableitung konstruktionsbedingt kontinuierlich sind und die dritte Ableitung an den Datenpunkten springt.

Monotone Interpolanten#

Kubische Splines sind konstruktionsbedingt zweimal stetig differenzierbar. Dies kann dazu führen, dass die Spline-Funktion zwischen den Datenpunkten oszilliert und "überschießt". In solchen Situationen ist es eine Alternative, die sogenannten *monotonen* kubischen Interpolanten zu verwenden: Diese sind so konstruiert, dass sie nur einmal stetig differenzierbar sind und versuchen, die durch die Daten implizierte lokale Form beizubehalten. scipy.interpolate bietet zwei Objekte dieser Art: PchipInterpolator und Akima1DInterpolator. Zur Veranschaulichung betrachten wir Daten mit einem Ausreißer.

>>> from scipy.interpolate import CubicSpline, PchipInterpolator, Akima1DInterpolator
>>> x = np.array([1., 2., 3., 4., 4.5, 5., 6., 7., 8])
>>> y = x**2
>>> y[4] += 101

>>> import matplotlib.pyplot as plt
>>> xx = np.linspace(1, 8, 51)
>>> plt.plot(xx, CubicSpline(x, y)(xx), '--', label='spline')
>>> plt.plot(xx, Akima1DInterpolator(x, y)(xx), '-', label='Akima1D')
>>> plt.plot(xx, PchipInterpolator(x, y)(xx), '-', label='pchip')
>>> plt.plot(x, y, 'o')
>>> plt.legend()
>>> plt.show()

Interpolation mit B-Splines#

B-Splines bilden eine alternative (wenn auch formal äquivalente) Darstellung von stückweisen Polynomen. Diese Basis ist im Allgemeinen rechnerisch stabiler als die Potenzbasis und nützlich für eine Vielzahl von Anwendungen, einschließlich Interpolation, Regression und Kurvendarstellung. Details finden Sie im Abschnitt stückweise Polynome, und hier veranschaulichen wir ihre Verwendung durch die Konstruktion der Interpolation einer Sinusfunktion.

>>> x = np.linspace(0, 3/2, 7)
>>> y = np.sin(np.pi*x)

Um die interpolierenden Objekte aus den Datenarrays x und y zu erstellen, verwenden wir die Funktion make_interp_spline.

>>> from scipy.interpolate import make_interp_spline
>>> bspl = make_interp_spline(x, y, k=3)

Diese Funktion gibt ein Objekt zurück, das eine ähnliche Schnittstelle wie die Objekte von CubicSpline aufweist. Insbesondere kann es an einem Datenpunkt ausgewertet und differenziert werden.

>>> der = bspl.derivative()      # a BSpline representing the derivative
>>> import matplotlib.pyplot as plt
>>> xx = np.linspace(0, 3/2, 51)
>>> plt.plot(xx, bspl(xx), '--', label=r'$\sin(\pi x)$ approx')
>>> plt.plot(x, y, 'o', label='data')
>>> plt.plot(xx, der(xx)/np.pi, '--', label=r'$d \sin(\pi x)/dx / \pi$ approx')
>>> plt.legend()
>>> plt.show()

Beachten Sie, dass wir durch die Angabe von k=3 im Aufruf von make_interp_spline einen kubischen Spline angefordert haben (dies ist der Standardwert, sodass k=3 hätte weggelassen werden können); die Ableitung eines kubischen Splines ist eine quadratische Funktion.

>>> bspl.k, der.k
(3, 2)

Standardmäßig ist das Ergebnis von make_interp_spline(x, y) äquivalent zu CubicSpline(x, y). Der Unterschied besteht darin, dass ersteres mehrere optionale Fähigkeiten ermöglicht: Es kann Splines verschiedener Grade (über das optionale Argument k) und vordefinierte Knoten (über das optionale Argument t) erstellen.

Randbedingungen für die Spline-Interpolation können durch das Argument bc_type an die Funktion make_interp_spline und den Konstruktor CubicSpline gesteuert werden. Standardmäßig verwenden beide die Randbedingung "not-a-knot".

Nicht-kubische Splines#

Eine Anwendung von make_interp_spline ist die Konstruktion eines linearen Interpolanten mit linearer Extrapolation, da make_interp_spline standardmäßig extrapoliert. Betrachten Sie

>>> from scipy.interpolate import make_interp_spline
>>> x = np.linspace(0, 5, 11)
>>> y = 2*x
>>> spl = make_interp_spline(x, y, k=1)  # k=1: linear
>>> spl([-1, 6])
[-2., 12.]
>>> np.interp([-1, 6], x, y)
[0., 10.]

Siehe den Abschnitt Extrapolation für weitere Details und Diskussionen.

Stapel von `y`#

Univariate Interpolatoren akzeptieren nicht nur eindimensionale y-Arrays, sondern auch solche mit y.ndim > 1. Die Interpretation ist, dass y ein *Stapel* von 1D-Datenarrays ist: Standardmäßig ist die nullte Dimension von y die Interpolationsachse, und die nachfolgenden Dimensionen sind Stapeldimensionen. Betrachten Sie eine Sammlung (einen *Stapel*) von Funktionen \(f_j\), die an den Punkten \(x_i\) abgetastet wurden. Wir können einen einzigen Interpolator für all diese Funktionen instanziieren, indem wir ein zweidimensionales Array y bereitstellen, so dass y[i, j] den Wert \(f_j(x_i)\) aufzeichnet.

Zur Veranschaulichung

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import make_interp_spline
>>> n = 11
>>> x = 2 * np.pi * np.arange(n) / n
>>> x.shape
(11,)
>>> y = np.stack((np.sin(x)**2, np.cos(x)), axis=1)
>>> y.shape
(11, 2)
>>> spl = make_interp_spline(x, y)
>>> xv = np.linspace(0, 2*np.pi, 51)
>>> plt.plot(x, y, 'o')
>>> plt.plot(xv, spl(xv), '-')
>>> plt.show()

Mehrere Anmerkungen sind angebracht. Erstens und vor allem sieht das Verhalten hier ähnlich wie beim Broadcasting von NumPy aus, unterscheidet sich aber in zwei Punkten.

Das Array x wird als 1D erwartet, auch wenn das Array y nicht 1D ist: x.ndim == 1, während y.ndim >= 1. Es gibt kein Broadcasting von x gegenüber y.
Standardmäßig werden die *nachfolgenden* Dimensionen als Stapeldimensionen verwendet, im Gegensatz zur NumPy-Konvention, bei der die *führenden* Dimensionen als Stapeldimensionen verwendet werden.

Zweitens kann die Interpolationsachse durch ein optionales Argument axis gesteuert werden. Das obige Beispiel verwendet den Standardwert axis=0. Für Nicht-Standardwerte gilt Folgendes:

y.shape[axis] == x.size (andernfalls wird ein Fehler ausgelöst)
Die Form von spl(xv) ist y.shape[axis:] + xv.shape + y.shape[:axis]

Obwohl wir das Stapelverhalten mit make_interp_spline demonstriert haben, unterstützen tatsächlich die meisten univariaten Interpolatoren diese Funktionalität: PchipInterpolator und Akima1DInterpolator, CubicSpline; niedrigstufige Polynomrepräsentationsklassen, PPoly, BPoly und BSpline; sowie Funktionen zur kleinsten Quadrate Anpassung und Spline-Glättung (Funktionen zur kleinsten Quadrate Anpassung und Spline-Glättung), make_lsq_spline und make_smoothing_spline.

Parametrische Spline-Kurven#

Bisher haben wir Spline- *Funktionen* betrachtet, bei denen erwartet wird, dass die Daten y explizit von der unabhängigen Variablen x abhängen – so dass die interpolierende Funktion \(f(x_j) = y_j\) erfüllt. Spline- *Kurven* behandeln die Arrays x und y als Koordinaten von Punkten, \(\mathbf{p}_j\) in einer Ebene, und eine interpolierende Kurve, die durch diese Punkte verläuft, wird durch einen zusätzlichen Parameter (typischerweise u genannt) parametrisiert. Beachten Sie, dass diese Konstruktion leicht auf höhere Dimensionen verallgemeinert werden kann, wo \(\mathbf{p}_j\) Punkte in einem N-dimensionalen Raum sind.

Spline-Kurven können leicht konstruiert werden, indem die Tatsache genutzt wird, dass Interpolationsfunktionen mehrdimensionale Datenarrays verarbeiten, wie im Abschnitt vorherigen Abschnitt besprochen. Die Werte des Parameters u, die den Datenpunkten entsprechen, müssen vom Benutzer separat angegeben werden.

Die Wahl der Parametrisierung ist problemabhängig und verschiedene Parametrisierungen können zu sehr unterschiedlichen Kurven führen. Als Beispiel betrachten wir drei Parametrisierungen eines (etwas schwierigen) Datensatzes, den wir aus Kapitel 6 von Referenz [1] im Docstring von BSpline entnehmen.

>>> x = [0, 1, 2, 3, 4, 5, 6]
>>> y = [0, 0, 0, 9, 0, 0, 0]
>>> p = np.stack((x, y))
>>> p
array([[0, 1, 2, 3, 4, 5, 6],
       [0, 0, 0, 9, 0, 0, 0]])

Wir nehmen Elemente des Arrays p als Koordinaten von sieben Punkten in der Ebene, wobei p[:, j] die Koordinaten des Punktes \(\mathbf{p}_j\) liefert.

Betrachten wir zuerst die *gleichmäßige* Parametrisierung, \(u_j = j\).

>>> u_unif = x

Zweitens betrachten wir die sogenannte *Sehnenlängen*-Parametrisierung, die nichts anderes ist als die kumulierte Länge von geradlinigen Segmenten, die die Datenpunkte verbinden.

\[u_j = u_{j-1} + |\mathbf{p}_j - \mathbf{p}_{j-1}|\]

für \(j=1, 2, \dots\) und \(u_0 = 0\). Hier ist \(| \cdots |\) die Länge zwischen den aufeinanderfolgenden Punkten \(p_j\) in der Ebene.

>>> dp = p[:, 1:] - p[:, :-1]      # 2-vector distances between points
>>> l = (dp**2).sum(axis=0)        # squares of lengths of 2-vectors between points
>>> u_cord = np.sqrt(l).cumsum()   # cumulative sums of 2-norms
>>> u_cord = np.r_[0, u_cord]      # the first point is parameterized at zero

Schließlich betrachten wir die manchmal als *zentripetal* bezeichnete Parametrisierung: \(u_j = u_{j-1} + |\mathbf{p}_j - \mathbf{p}_{j-1}|^{1/2}\). Aufgrund der zusätzlichen Quadratwurzel wird der Unterschied zwischen aufeinanderfolgenden Werten \(u_j - u_{j-1}\) kleiner sein als bei der Sehnenlängen-Parametrisierung.

>>> u_c = np.r_[0, np.cumsum((dp**2).sum(axis=0)**0.25)]

Nun plotten wir die resultierenden Kurven.

>>> from scipy.interpolate import make_interp_spline
>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots(1, 3, figsize=(8, 3))
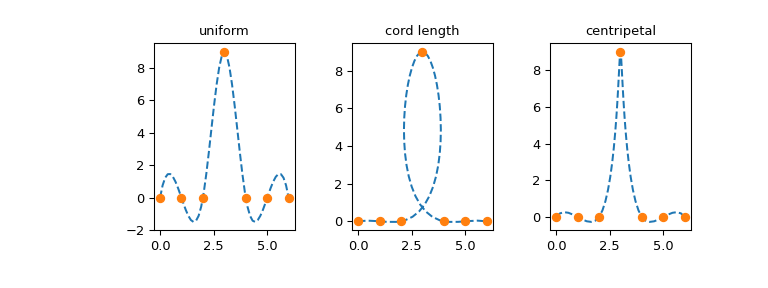
>>> parametrizations = ['uniform', 'cord length', 'centripetal']
>>>
>>> for j, u in enumerate([u_unif, u_cord, u_c]):
...    spl = make_interp_spline(u, p, axis=1)    # note p is a 2D array
...
...    uu = np.linspace(u[0], u[-1], 51)
...    xx, yy = spl(uu)
...
...    ax[j].plot(xx, yy, '--')
...    ax[j].plot(p[0, :], p[1, :], 'o')
...    ax[j].set_title(parametrizations[j])
>>> plt.show()

Fehlende Daten#

Wir weisen darauf hin, dass scipy.interpolate *keine* Interpolation mit fehlenden Daten unterstützt. Zwei gängige Arten der Darstellung fehlender Daten sind die Verwendung von Masked Arrays aus der numpy.ma-Bibliothek und die Kodierung fehlender Werte als "nicht-eine-Zahl", NaN.

Keiner dieser beiden Ansätze wird direkt in scipy.interpolate unterstützt. Einzelne Routinen können teilweise Unterstützung und/oder Workarounds bieten, aber im Allgemeinen hält sich die Bibliothek fest an die IEEE 754-Semantik, bei der ein NaN für *nicht-eine-Zahl* steht, d.h. das Ergebnis einer ungültigen mathematischen Operation (z.B. Division durch Null), nicht für *fehlend*.

Legacy-Schnittstelle für 1-D-Interpolation (`interp1d`)#

Hinweis

interp1d gilt als Legacy-API und wird für die Verwendung in neuem Code nicht empfohlen. Erwägen Sie die Verwendung von spezifischeren Interpolatoren stattdessen.

Die Klasse interp1d in scipy.interpolate ist eine bequeme Methode, um eine Funktion basierend auf festen Datenpunkten zu erstellen, die innerhalb des durch die gegebenen Daten definierten Bereichs überall ausgewertet werden kann, wobei lineare Interpolation verwendet wird. Eine Instanz dieser Klasse wird durch Übergabe der 1-D-Vektoren, die die Daten bilden, erstellt. Die Instanz dieser Klasse definiert eine Methode __call__ und kann daher wie eine Funktion behandelt werden, die zwischen bekannten Datenwerten interpoliert, um unbekannte Werte zu erhalten. Das Verhalten am Rand kann zum Zeitpunkt der Instanziierung spezifiziert werden. Das folgende Beispiel demonstriert die Verwendung für lineare und kubische Spline-Interpolation.

>>> from scipy.interpolate import interp1d

>>> x = np.linspace(0, 10, num=11, endpoint=True)
>>> y = np.cos(-x**2/9.0)
>>> f = interp1d(x, y)
>>> f2 = interp1d(x, y, kind='cubic')

>>> xnew = np.linspace(0, 10, num=41, endpoint=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
>>> plt.legend(['data', 'linear', 'cubic'], loc='best')
>>> plt.show()

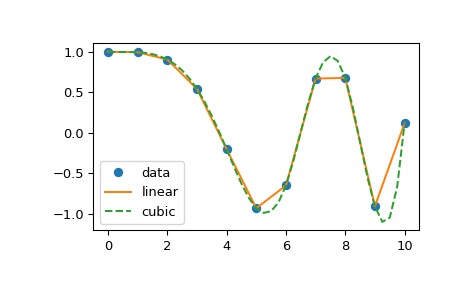
"This code generates an X-Y plot of a time-series with amplitude on the Y axis and time on the X axis. The original time-series is shown as a series of blue markers roughly defining some kind of oscillation. An orange trace showing the linear interpolation is drawn atop the data forming a jagged representation of the original signal. A dotted green cubic interpolation is also drawn that appears to smoothly represent the source data."

Die 'cubic'-Art von interp1d ist äquivalent zu make_interp_spline, und die 'linear'-Art ist äquivalent zu numpy.interp, erlaubt aber auch N-dimensionale y-Arrays.

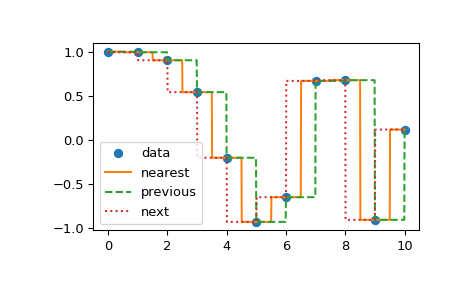
Eine weitere Reihe von Interpolationen in interp1d sind *nearest*, *previous* und *next*, bei denen die nächstgelegenen, vorherigen oder nächsten Punkte entlang der x-Achse zurückgegeben werden. Nearest und next können als Sonderfall eines kausalen interpolierenden Filters betrachtet werden. Das folgende Beispiel demonstriert ihre Verwendung unter Verwendung derselben Daten wie im vorherigen Beispiel.

>>> from scipy.interpolate import interp1d

>>> x = np.linspace(0, 10, num=11, endpoint=True)
>>> y = np.cos(-x**2/9.0)
>>> f1 = interp1d(x, y, kind='nearest')
>>> f2 = interp1d(x, y, kind='previous')
>>> f3 = interp1d(x, y, kind='next')

>>> xnew = np.linspace(0, 10, num=1001, endpoint=True)
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o')
>>> plt.plot(xnew, f1(xnew), '-', xnew, f2(xnew), '--', xnew, f3(xnew), ':')
>>> plt.legend(['data', 'nearest', 'previous', 'next'], loc='best')
>>> plt.show()

Empfohlene Ersatz für `interp1d`-Modi#

Wie bereits erwähnt, ist die Klasse interp1d *Legacy*: Wir haben keine Pläne, sie zu entfernen; wir werden ihre bestehenden Verwendungen weiterhin unterstützen; wir glauben jedoch, dass es bessere Alternativen gibt, deren Verwendung wir in neuem Code empfehlen.

Hier listen wir spezifische Empfehlungen auf, abhängig von der Interpolationsart kind.

Lineare Interpolation, kind="linear"

Die Standardempfehlung ist die Verwendung der Funktion numpy.interp. Alternativ können Sie lineare Splines verwenden, make_interp_spline(x, y, k=1), siehe diesen Abschnitt zur Diskussion.

Spline-Interpolatoren, kind="quadratic" oder "cubic"

Intern delegiert interp1d an make_interp_spline, daher empfehlen wir, letztere direkt zu verwenden.

Stückweise konstante Modi, kind="nearest", "previous", "next"

Zuerst stellen wir fest, dass interp1d(x, y, kind='previous') äquivalent zu make_interp_spline(x, y, k=0) ist.

Allgemeiner jedoch basieren alle diese stückweise konstanten Interpolationsmodi auf numpy.searchsorted. Zum Beispiel ist der Modus "nearest" nichts anderes als.

>>> x = np.arange(8)
>>> y = x**2
>>> x_new = np.linspace(0, 7, 101)    # input points
>>> x_bds = x[:-1] / 2.0 + x[1:] / 2.0   # halfway points
>>> idx = np.searchsorted(x_bds, x_new, side='left')
>>> idx = np.clip(idx, 0, len(x) - 1)  # clip the indices so that they are within the range of x indices.
>>> import matplotlib.pyplot as plt
>>> plt.plot(x, y, 'o')
>>> plt.plot(x_new, y[idx], '--')
>>> plt.show()

Andere Varianten sind ähnlich, siehe den Quellcode von interp1d für Details.