Stückweise Polynome und Splines#
Die 1D-Interpolationsroutinen, die im vorherigen Abschnitt besprochen wurden, arbeiten durch die Konstruktion bestimmter stückweiser Polynome: Der Interpolationsbereich wird durch die sogenannten Bruchpunkte in Intervalle aufgeteilt, und auf jedem Intervall gibt es ein bestimmtes Polynom. Diese Polynomstücke passen dann an den Bruchpunkten mit einer vordefinierten Glattheit überein: die zweiten Ableitungen für kubische Splines, die ersten Ableitungen für monotone Interpolanten und so weiter.
Ein Polynom vom Grad \(k\) kann als Linearkombination von \(k+1\) monomialen Basiselementen, \(1, x, x^2, \cdots, x^k\), betrachtet werden. In einigen Anwendungen ist es nützlich, alternative (wenn auch formal äquivalente) Basen zu betrachten. Zwei beliebte Basen, die in scipy.interpolate implementiert sind, sind B-Splines (BSpline) und Bernstein-Polynome (BPoly). B-Splines werden oft beispielsweise für nichtparametrische Regressionsprobleme verwendet, und Bernstein-Polynome werden für die Konstruktion von Bézier-Kurven verwendet.
PPoly-Objekte repräsentieren stückweise Polynome in der „üblichen“ Potenzbasis. Dies ist der Fall bei Instanzen von CubicSpline und monotonen Interpolanten. Im Allgemeinen können PPoly-Objekte Polynome beliebiger Ordnungen darstellen, nicht nur kubische. Für das Datenarray x befinden sich die Bruchpunkte an den Datenpunkten, und das Koeffizientenarray c definiert Polynome vom Grad \(k\), sodass c[i, j] ein Koeffizient für (x - x[j])**(k-i) auf dem Segment zwischen x[j] und x[j+1] ist.
BSpline-Objekte repräsentieren B-Spline-Funktionen — Linearkombinationen von B-Spline-Basiselementen. Diese Objekte können direkt instanziiert oder aus Daten mit der Factory-Funktion make_interp_spline erstellt werden.
Schließlich werden Bernstein-Polynome als Instanzen der Klasse BPoly repräsentiert.
Alle diese Klassen implementieren eine (meistens) ähnliche Schnittstelle, wobei PPoly die umfangreichste ist. Im Folgenden betrachten wir die Hauptmerkmale dieser Schnittstelle und diskutieren einige Details der alternativen Basen für stückweise Polynome.
Bearbeiten von PPoly-Objekten#
PPoly-Objekte verfügen über praktische Methoden zur Konstruktion von Ableitungen und Stammfunktionen, zur Berechnung von Integralen und zur Nullstellensuche. Wir tabellieren beispielsweise die Sinusfunktion und finden die Nullstellen ihrer Ableitung.
>>> import numpy as np
>>> from scipy.interpolate import CubicSpline
>>> x = np.linspace(0, 10, 71)
>>> y = np.sin(x)
>>> spl = CubicSpline(x, y)
Differenzieren Sie nun den Spline
>>> dspl = spl.derivative()
Hier ist dspl eine PPoly-Instanz, die eine Polynomapproximation der Ableitung des ursprünglichen Objekts, spl, darstellt. Die Auswertung von dspl an einem festen Argument ist äquivalent zur Auswertung des ursprünglichen Splines mit dem Argument nu=1.
>>> dspl(1.1), spl(1.1, nu=1)
(0.45361436, 0.45361436)
Beachten Sie, dass die zweite Form oben die Ableitung inplace auswertet, während wir mit dem Objekt dspl die Nullstellen der Ableitung von spl finden können.
>>> dspl.roots() / np.pi
array([-0.45480801, 0.50000034, 1.50000099, 2.5000016 , 3.46249993])
Dies stimmt gut mit den Nullstellen \(\pi/2 + \pi\,n\) von \(\cos(x) = \sin'(x)\) überein. Beachten Sie, dass standardmäßig die Nullstellen extrapoliert außerhalb des Interpolationsintervalls \(0 \leqslant x \leqslant 10\) berechnet wurden und dass die extrapolierten Ergebnisse (der erste und der letzte Wert) viel weniger genau sind. Wir können die Extrapolation ausschalten und die Nullstellensuche auf das Interpolationsintervall beschränken.
>>> dspl.roots(extrapolate=False) / np.pi
array([0.50000034, 1.50000099, 2.5000016])
Tatsächlich ist die Methode root ein Spezialfall einer allgemeineren Methode solve, die für eine gegebene Konstante \(y\) die Lösungen der Gleichung \(f(x) = y\) findet, wobei \(f(x)\) das stückweise Polynom ist.
>>> dspl.solve(0.5, extrapolate=False) / np.pi
array([0.33332755, 1.66667195, 2.3333271])
was gut mit den erwarteten Werten von \(\pm\arccos(1/2) + 2\pi\,n\) übereinstimmt.
Integrale von stückweisen Polynomen können mit der Methode .integrate berechnet werden, die die untere und obere Integrationsgrenze akzeptiert. Als Beispiel berechnen wir eine Approximation des vollständigen elliptischen Integrals \(K(m) = \int_0^{\pi/2} [1 - m\sin^2 x]^{-1/2} dx\).
>>> from scipy.special import ellipk
>>> m = 0.5
>>> ellipk(m)
1.8540746773013719
Zu diesem Zweck tabellieren wir den Integranden und interpolieren ihn mit dem monotonen PCHIP-Interpolanten (wir könnten auch einen CubicSpline verwenden).
>>> from scipy.interpolate import PchipInterpolator
>>> x = np.linspace(0, np.pi/2, 70)
>>> y = (1 - m*np.sin(x)**2)**(-1/2)
>>> spl = PchipInterpolator(x, y)
und integrieren
>>> spl.integrate(0, np.pi/2)
1.854074674965991
was tatsächlich nahe am von scipy.special.ellipk berechneten Wert liegt.
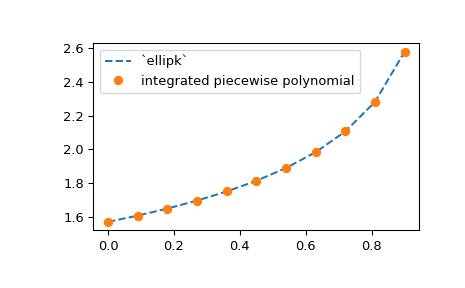
Alle stückweisen Polynome können mit N-dimensionalen y-Werten konstruiert werden. Wenn y.ndim > 1, wird dies als Stapel von 1D- y-Werten verstanden, die entlang der Interpolationsachse (mit dem Standardwert 0) angeordnet sind. Letztere wird über das Argument axis spezifiziert, und die Invariante ist, dass len(x) == y.shape[axis]. Als Beispiel erweitern wir das obige elliptische Integralbeispiel, um die Approximation für einen Bereich von m-Werten zu berechnen, unter Verwendung des NumPy-Broadcasting.
>>> from scipy.interpolate import PchipInterpolator
>>> m = np.linspace(0, 0.9, 11)
>>> x = np.linspace(0, np.pi/2, 70)
>>> y = 1 / np.sqrt(1 - m[:, None]*np.sin(x)**2)
Nun hat das y-Array die Form (11, 70), sodass die Werte von y für einen festen Wert von m entlang der zweiten Achse des y-Arrays liegen.
>>> spl = PchipInterpolator(x, y, axis=1) # the default is axis=0
>>> import matplotlib.pyplot as plt
>>> plt.plot(m, spl.integrate(0, np.pi/2), '--')
>>> from scipy.special import ellipk
>>> plt.plot(m, ellipk(m), 'o')
>>> plt.legend(['`ellipk`', 'integrated piecewise polynomial'])
>>> plt.show()
B-Splines: Knoten und Koeffizienten#
Eine B-Spline-Funktion — beispielsweise konstruiert aus Daten über einen Aufruf von make_interp_spline — wird durch die sogenannten Knoten und Koeffizienten definiert.
Zur Veranschaulichung konstruieren wir erneut die Interpolation einer Sinusfunktion. Die Knoten sind als Attribut t einer BSpline-Instanz verfügbar.
>>> x = np.linspace(0, 3/2, 7)
>>> y = np.sin(np.pi*x)
>>> from scipy.interpolate import make_interp_spline
>>> bspl = make_interp_spline(x, y, k=3)
>>> print(bspl.t)
[0. 0. 0. 0. 0.5 0.75 1. 1.5 1.5 1.5 1.5 ]
>>> print(x)
[ 0. 0.25 0.5 0.75 1. 1.25 1.5 ]
Wir sehen, dass der Knotenvektor standardmäßig aus dem Eingabearray x konstruiert wird: Zuerst wird er \((k+1)\)-regulär gemacht (er hat k wiederholte Knoten, die angehängt und vorangestellt werden); dann werden der zweite und der vorletzte Punkt des Eingabearrays entfernt – dies ist die sogenannte Not-a-Knot-Randbedingung.
Im Allgemeinen benötigt ein interpolierender Spline vom Grad k len(t) - len(x) - k - 1 Randbedingungen. Für kubische Splines mit (k+1)-regulären Knotenarrays bedeutet dies zwei Randbedingungen – oder das Entfernen zweier Werte aus dem x-Array. Verschiedene Randbedingungen können mit dem optionalen Argument bc_type von make_interp_spline angefordert werden.
Die B-Spline-Koeffizienten werden über das Attribut c eines BSpline-Objekts abgerufen.
>>> len(bspl.c)
7
Die Konvention ist, dass es für len(t) Knoten len(t) - k - 1 Koeffizienten gibt. Einige Routinen (siehe Abschnitt Glättende Splines) polstern die c-Arrays mit Nullen auf, sodass len(c) == len(t). Diese zusätzlichen Koeffizienten werden bei der Auswertung ignoriert.
Wir betonen, dass die Koeffizienten in der B-Spline-Basis angegeben sind, nicht in der Potenzbasis von \(1, x, \cdots, x^k\).
B-Spline-Basiselemente#
Die B-Spline-Basis wird in einer Vielzahl von Anwendungen verwendet, darunter Interpolation, Regression und Kurvenrepräsentation. B-Splines sind stückweise Polynome, die als Linearkombinationen von B-Spline-Basiselementen dargestellt werden – welche selbst bestimmte Linearkombinationen üblicher Monome, \(x^m\) mit \(m=0, 1, \dots, k\), sind.
Die Eigenschaften von B-Splines sind in der Literatur gut beschrieben (siehe zum Beispiel die Referenzen in der BSpline-Docstring). Für unsere Zwecke reicht es aus zu wissen, dass eine B-Spline-Funktion eindeutig durch ein Koeffizientenarray und ein Array der sogenannten Knoten definiert ist, die mit den Datenpunkten x übereinstimmen können oder auch nicht.
Konkret ist ein B-Spline-Basiselement vom Grad k (z. B. k=3 für kubische) durch \(k+2\) Knoten definiert und außerhalb dieser Knoten null. Zur Veranschaulichung plotten wir eine Sammlung von nicht-null Basiselementen auf einem bestimmten Intervall.
>>> k = 3 # cubic splines
>>> t = [0., 1.4, 2., 3.1, 5.] # internal knots
>>> t = np.r_[[0]*k, t, [5]*k] # add boundary knots
>>> from scipy.interpolate import BSpline
>>> import matplotlib.pyplot as plt
>>> for j in [-2, -1, 0, 1, 2]:
... a, b = t[k+j], t[-k+j-1]
... xx = np.linspace(a, b, 101)
... bspl = BSpline.basis_element(t[k+j:-k+j])
... plt.plot(xx, bspl(xx), label=f'j = {j}')
>>> plt.legend(loc='best')
>>> plt.show()
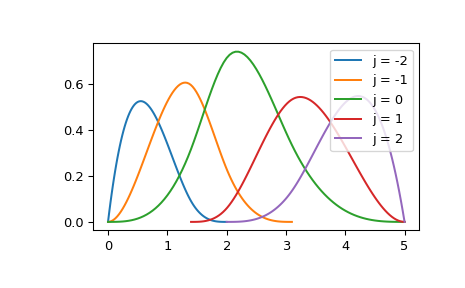
Hier ist BSpline.basis_element im Wesentlichen eine Abkürzung für die Konstruktion eines Splines mit nur einem nicht-null Koeffizienten. Zum Beispiel ist das j=2-Element im obigen Beispiel äquivalent zu.
>>> c = np.zeros(t.size - k - 1)
>>> c[-2] = 1
>>> b = BSpline(t, c, k)
>>> np.allclose(b(xx), bspl(xx))
True
Bei Bedarf kann ein B-Spline mit der Methode PPoly.from_spline in ein PPoly-Objekt konvertiert werden, die eine BSpline-Instanz akzeptiert und eine PPoly-Instanz zurückgibt. Die umgekehrte Konvertierung erfolgt durch die Methode BSpline.from_power_basis. Konvertierungen zwischen Basen sollten jedoch am besten vermieden werden, da sie Rundungsfehler ansammeln.
Design-Matrizen in der B-Spline-Basis#
Eine gängige Anwendung von B-Splines ist die nichtparametrische Regression. Der Grund dafür ist, dass die lokalisierte Natur der B-Spline-Basiselemente die lineare Algebra bandförmig macht. Das liegt daran, dass höchstens \(k+1\) Basiselemente an einem gegebenen Auswertungspunkt nicht null sind, daher hat eine auf B-Splines aufgebaute Design-Matrix höchstens \(k+1\) Diagonalen.
Zur Veranschaulichung betrachten wir ein Spielzeugbeispiel. Angenommen, unsere Daten sind eindimensional und beschränkt auf ein Intervall \([0, 6]\). Wir konstruieren einen 4-regulären Knotenvektor, der 7 Datenpunkte und kubische Splines vom Grad k=3 entspricht.
>>> t = [0., 0., 0., 0., 2., 3., 4., 6., 6., 6., 6.]
Nehmen Sie als Nächstes „Beobachtungen“:
>>> xnew = [1, 2, 3]
und konstruieren Sie die Design-Matrix im spärlichen CSR-Format.
>>> from scipy.interpolate import BSpline
>>> mat = BSpline.design_matrix(xnew, t, k=3)
>>> mat
<Compressed Sparse Row sparse array of dtype 'float64'
with 12 stored elements and shape (3, 7)>
Hier entspricht jede Zeile der Design-Matrix einem Wert im Array xnew, und eine Zeile hat nicht mehr als k+1 = 4 Nicht-Null-Elemente; Zeile j enthält Basiselemente, die an xnew[j] ausgewertet werden.
>>> with np.printoptions(precision=3):
... print(mat.toarray())
[[0.125 0.514 0.319 0.042 0. 0. 0. ]
[0. 0.111 0.556 0.333 0. 0. 0. ]
[0. 0. 0.125 0.75 0.125 0. 0. ]]
Bernstein-Polynome, BPoly#
Für \(t \in [0, 1]\) sind Bernstein-Basispolynome vom Grad \(k\) definiert durch:
wobei \(C_k^a\) der Binomialkoeffizient ist und \(a=0, 1, \dots, k\), sodass es \(k+1\) Basispolynome vom Grad \(k\) gibt.
Ein BPoly-Objekt repräsentiert ein stückweises Bernstein-Polynom in Bezug auf Bruchpunkte x und Koeffizienten c: c[a, j] gibt den Koeffizienten für \(b(t; k, a)\) für t im Intervall zwischen x[j] und x[j+1] an.
Die Benutzeroberfläche von BPoly-Objekten ist der von PPoly-Objekten sehr ähnlich: Beide können ausgewertet, differenziert und integriert werden.
Eine zusätzliche Funktion von BPoly-Objekten ist der alternative Konstruktor BPoly.from_derivatives, der ein BPoly-Objekt aus Datenwerten und Ableitungen konstruiert. Spezifisch gibt b = BPoly.from_derivatives(x, y) eine aufrufbare Funktion zurück, die die bereitgestellten Werte interpoliert, b(x[i]) == y[i]), und die bereitgestellten Ableitungen hat, b(x[i], nu=j) == y[i][j].
Diese Operation ähnelt CubicHermiteSpline, ist aber flexibler, da sie unterschiedliche Anzahlen von Ableitungen an verschiedenen Datenpunkten verarbeiten kann; d. h., das Argument y kann eine Liste von Arrays unterschiedlicher Längen sein. Siehe BPoly.from_derivatives für weitere Diskussionen und Beispiele.
Konvertierung zwischen Basen#
Im Prinzip sind alle drei Basen für stückweise Polynome (die Potenzbasis, die Bernstein-Basis und B-Splines) äquivalent, und ein Polynom in einer Basis kann in eine andere Basis konvertiert werden. Ein Grund für die Konvertierung zwischen Basen ist, dass nicht alle Basen alle Operationen implementieren. Zum Beispiel ist die Nullstellensuche nur für PPoly implementiert, und daher müssen Sie, um Nullstellen eines BSpline-Objekts zu finden, zuerst nach PPoly konvertieren. Siehe die Methoden PPoly.from_bernstein_basis, PPoly.from_spline, BPoly.from_power_basis und BSpline.from_power_basis für Details zur Konvertierung.
In Gleitkommaarithmetik führen Konvertierungen jedoch immer zu einem gewissen Präzisionsverlust. Ob dies signifikant ist, hängt vom Problem ab, daher wird empfohlen, bei der Konvertierung zwischen Basen vorsichtig zu sein.