Random Variable Transition Guide#
Hintergrund#
Vor SciPy 1.15 waren alle kontinuierlichen Wahrscheinlichkeitsverteilungen von SciPy (z. B. scipy.stats.norm) Instanzen von Unterklassen von scipy.stats.rv_continuous.
from scipy import stats
dist = stats.norm
type(dist)
scipy.stats._continuous_distns.norm_gen
isinstance(dist, stats.rv_continuous)
True
Es gab zwei offensichtliche Möglichkeiten, mit diesen Objekten zu arbeiten.
Nach der gebräuchlicheren Methode wurden sowohl "Argumente" (z. B. x) als auch "Verteilungsparameter" (z. B. loc, scale) als Eingaben für Methoden des Objekts bereitgestellt.
x, loc, scale = 1., 0., 1.
dist.pdf(x, loc, scale)
np.float64(0.24197072451914337)
Der weniger gebräuchliche Ansatz bestand darin, die Methode __call__ des Verteilungsobjekts aufzurufen, die unabhängig von der ursprünglichen Klasse eine Instanz von rv_continuous_frozen zurückgab.
frozen = stats.norm()
type(frozen)
scipy.stats._distn_infrastructure.rv_continuous_frozen
Methoden dieses neuen Objekts akzeptieren nur Argumente, keine Verteilungsparameter.
frozen.pdf(x)
np.float64(0.24197072451914337)
In gewissem Sinne stellten die Instanzen von rv_continuous wie norm "Verteilungsfamilien" dar, die Parameter zur Identifizierung einer bestimmten Wahrscheinlichkeitsverteilung benötigen, und eine Instanz von rv_continuous_frozen war ähnlich einer "Zufallsvariable" - ein mathematisches Objekt, das einer bestimmten Wahrscheinlichkeitsverteilung folgt.
Beide Ansätze sind gültig und haben in bestimmten Situationen Vorteile. Zum Beispiel erscheint stats.norm.pdf(x) natürlicher als stats.norm().pdf(x) für eine so einfache Abfrage oder wenn Methoden als Funktionen von Verteilungsparametern und nicht als übliche Argumente (z. B. Likelihood) betrachtet werden. Der erstere Ansatz hat jedoch einige inhärente Nachteile; z. B. müssen alle 125 kontinuierlichen Verteilungen von SciPy beim Import instanziiert werden, Verteilungsparameter müssen jedes Mal validiert werden, wenn eine Methode aufgerufen wird, und die Dokumentation von Methoden muss entweder a) separat für jede Methode jeder Verteilung generiert werden oder b) die für jede Verteilung eindeutigen Formparameter weglassen. Um diese und andere Mängel zu beheben, schlug gh-15928 eine neue, separate Infrastruktur vor, die auf dem letzteren (Zufallsvariablen-) Ansatz basiert. Dieser Übergangsleitfaden dokumentiert, wie Benutzer von rv_continuous und rv_continuous_frozen zur neuen Infrastruktur migrieren können.
Hinweis: Die neue Infrastruktur ist für einige Anwendungsfälle möglicherweise noch nicht so bequem, insbesondere für die Anpassung von Verteilungsparametern an Daten. Benutzer können die alte Infrastruktur weiterhin verwenden, wenn sie ihren Bedürfnissen entspricht; sie ist derzeit nicht veraltet.
Grundlagen#
In der neuen Infrastruktur heißen Verteilungsfamilien Klassen gemäß der CamelCase-Konvention. Sie müssen vor der Verwendung instanziiert werden, wobei Parameter als schlüsselwortorientierte Argumente übergeben werden. *Instanzen* der Verteilungsfamilienklassen können als Zufallsvariablen betrachtet werden, die in der Mathematik üblicherweise mit Großbuchstaben bezeichnet werden.
from scipy import stats
mu, sigma = 0, 1
X = stats.Normal(mu=mu, sigma=sigma)
X
Normal(mu=np.float64(0.0), sigma=np.float64(1.0))
Nach der Instanziierung können Formparameter als Attribute gelesen (aber nicht geschrieben) werden.
X.mu, X.sigma
(np.float64(0.0), np.float64(1.0))
Die Dokumentation von scipy.stats.Normal enthält Links zur detaillierten Dokumentation jeder ihrer Methoden. (Vergleichen Sie beispielsweise mit der Dokumentation von scipy.stats.norm.)
Hinweis: Obwohl nur Normal und Uniform ab SciPy 1.15 eine gerenderte Dokumentation haben und direkt aus stats importiert werden können, können fast alle anderen alten Verteilungen über make_distribution (bald besprochen) mit der neuen Schnittstelle verwendet werden.
Methoden werden dann aufgerufen, indem nur das bzw. die Argumente übergeben werden, falls vorhanden, nicht die Verteilungsparameter.
X.mean()
np.float64(0.0)
X.pdf(x)
np.float64(0.24197072451914337)
Bei einfachen Aufrufen wie diesem (z. B. wenn das Argument eine gültige Gleitkommazahl ist) sind Aufrufe von Methoden der neuen Zufallsvariablen typischerweise schneller als vergleichbare Aufrufe von alten Verteilungsmethoden.
%timeit X.pdf(x)
2.44 μs ± 1.49 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%timeit frozen.pdf(x)
17.2 μs ± 39.4 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%timeit dist.pdf(x, loc=mu, scale=sigma)
17.4 μs ± 185 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Beachten Sie, dass die Art und Weise, wie X.pdf und frozen.pdf aufgerufen werden, identisch ist, und der Aufruf von dist.pdf sehr ähnlich ist – der einzige Unterschied besteht darin, dass der Aufruf von dist.pdf die Formparameter enthält, während in der neuen Infrastruktur die Formparameter nur bei der Instanziierung der Zufallsvariable übergeben werden.
Neben pdf und mean sind mehrere andere Methoden der neuen Infrastruktur im Wesentlichen dieselben wie die alten Methoden.
logpdf(Logarithmus der Wahrscheinlichkeitsdichtefunktion)cdf(kumulative Verteilungsfunktion)logcdf(Logarithmus der kumulativen Verteilungsfunktion)entropy(differentielle Entropie)mediansupport
Andere Methoden haben neue Namen, sind aber ansonsten Drop-in-Ersatz.
sf(Überlebensfunktion) \(\rightarrow\)ccdf(komplementäre kumulative Verteilungsfunktion)logsf\(\rightarrow\)logccdfppf(Perzentil-Punkt-Funktion) \(\rightarrow\)icdf(inverse kumulative Verteilungsfunktion)isf(inverse Überlebensfunktion) \(\rightarrow\)iccdf(inverse komplementäre kumulative Verteilungsfunktion)std\(\rightarrow\)standard_deviationvar\(\rightarrow\)variance
Die neue Infrastruktur hat mehrere *neue* Methoden in der gleichen Art wie die oben genannten.
ilogcdf(Inverse des Logarithmus der kumulativen Verteilungsfunktion)ilogccdf(Inverse des Logarithmus der komplementären kumulativen Verteilungsfunktion)logentropy(Logarithmus der Entropie)mode(Modus der Verteilung)Schiefekurtosis( *nicht-exzessive* Kurtosis; siehe "Standardisierte Momente" unten)
Und sie hat eine neue plot-Methode zur Bequemlichkeit
import matplotlib.pyplot as plt
X.plot()
plt.show()
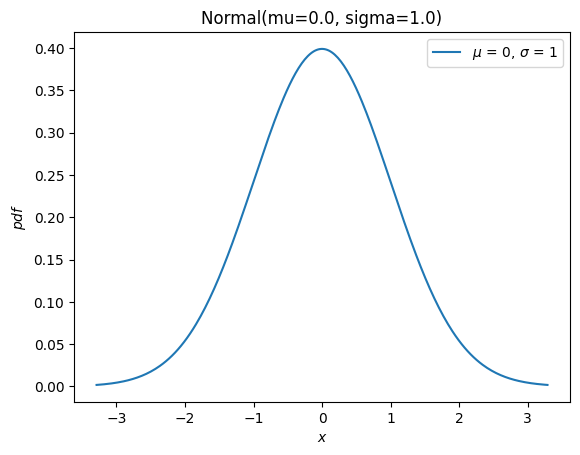
Die meisten der verbleibenden Methoden der alten Infrastruktur (rvs, moment, stats, interval, fit, nnlf, fit_loc_scale und expect) haben eine analoge Funktionalität, aber einige Sorgfalt ist erforderlich. Bevor die Ersetzungen beschrieben werden, erwähnen wir kurz, wie mit Zufallsvariablen gearbeitet werden kann, die nicht normalverteilt sind: Fast alle alten Verteilungsobjekte können mit scipy.stats.make_distribution in eine neue Verteilungsklasse konvertiert werden, und die neue Verteilungsklasse kann durch Übergabe der Formparameter als Schlüsselwortargumente instanziiert werden. Betrachten Sie zum Beispiel die Weibull-Verteilung. Wir können eine neue Klasse erstellen, die eine Abstraktion der Verteilungsfamilie darstellt, wie
Weibull = stats.make_distribution(stats.weibull_min)
print(Weibull.__doc__[:288]) # help(Weibull) prints this and (too much) more
This class represents `scipy.stats.weibull_min` as a subclass of `<class 'scipy.stats._distribution_infrastructure.ContinuousDistribution'>`.
The `repr`/`str` of class instances is `Weibull`.
The PDF of the distribution is defined for :math:`x \in [0.0, \infty]`.
This class accepts one p
Gemäß der Dokumentation von weibull_min wird der Formparameter mit c bezeichnet, so dass wir eine Zufallsvariable instanziieren können, indem wir c als Schlüsselwortargument an die neue Weibull-Klasse übergeben.
c = 2.
X = Weibull(c=c)
X.plot()
plt.show()
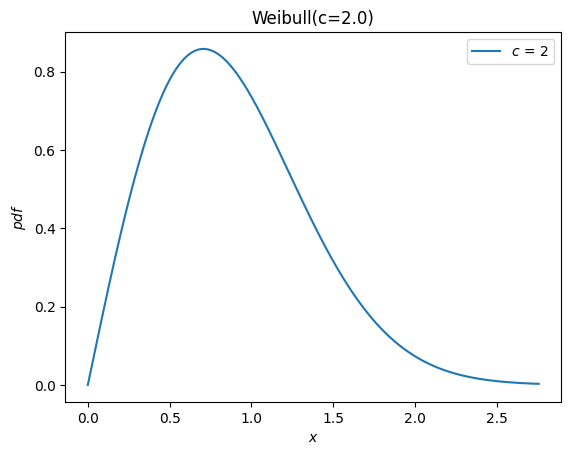
Zuvor erbten alle Verteilungen die Verteilungsparameter loc und scale. *Diese werden nicht mehr akzeptiert*. Stattdessen können Zufallsvariablen mit arithmetischen Operatoren verschoben und skaliert werden.
Y = 2*X + 1
Y.plot() # note the change in the abscissae
plt.show()
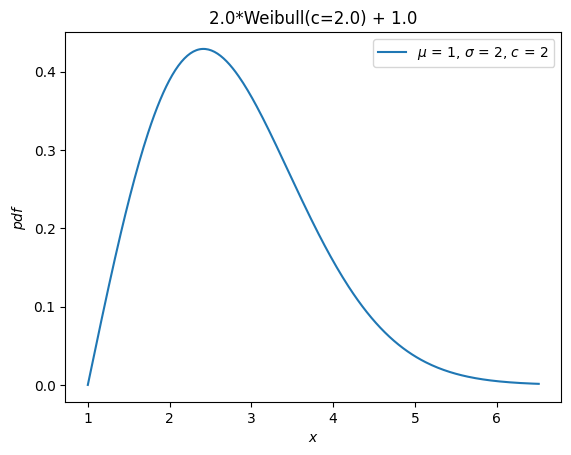
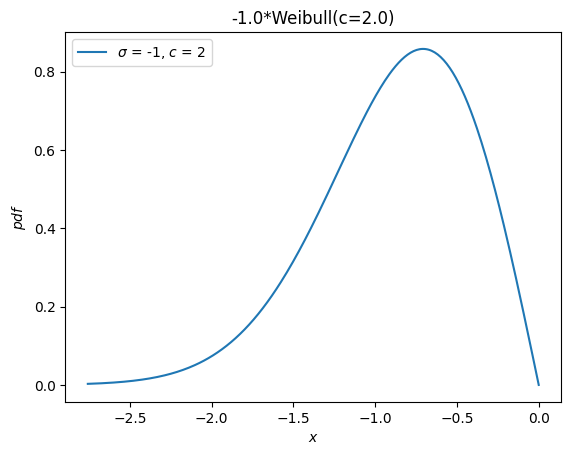
Eine separate Verteilung, weibull_max, wurde als Spiegelbild von weibull_min um den Ursprung bereitgestellt. Nun ist dies einfach -X.
Y = -X
Y.plot()
plt.show()
Momente#
Die alte Infrastruktur bietet eine moments-Methode für rohe Momente. Wenn nur die Ordnung angegeben wird, ist die neue moment-Methode ein Drop-in-Ersatz.
stats.weibull_min.moment(1, c), X.moment(1) # first raw moment of the Weibull distribution with shape c
(np.float64(0.8862269254527579), np.float64(0.8862269254527579))
Die alte Infrastruktur hat jedoch auch eine stats-Methode, die verschiedene Statistiken der Verteilung lieferte. Die folgenden Statistiken waren mit den angegebenen Zeichen verbunden.
Mittelwert (erster roher Moment um den Ursprung,
'm')Varianz (zweiter zentraler Moment,
'v')Schiefe (dritter standardisierter Moment,
's')Exzess-Kurtosis (vierter standardisierter Moment minus 3,
'k')
Zum Beispiel
stats.weibull_min.stats(c, moments='mvsk')
(np.float64(0.8862269254527579),
np.float64(0.21460183660255183),
np.float64(0.6311106578189344),
np.float64(0.24508930068764556))
Nun können Momente beliebiger order und kind (roh, zentral und standardisiert) berechnet werden, indem die entsprechenden Argumente an die neue moment-Methode übergeben werden.
(X.moment(order=1, kind='raw'),
X.moment(order=2, kind='central'),
X.moment(order=3, kind='standardized'),
X.moment(order=4, kind='standardized'))
(np.float64(0.8862269254527579),
np.float64(0.21460183660255183),
np.float64(0.6311106578189344),
np.float64(3.2450893006876314))
Beachten Sie den Unterschied in der Definition von Kurtosis. Zuvor wurde die "Exzess-" (auch "Fisher'sche") Kurtosis geliefert. Gemäß Konvention (statt der natürlichen mathematischen Definition) ist dies der standardisierte vierte Moment, der um eine Konstante ( 3) verschoben wird, um für die Normalverteilung den Wert 0.0 zu ergeben.
stats.norm.stats(moments='k')
np.float64(0.0)
Die neuen Methoden moment und kurtosis halten sich standardmäßig nicht an diese Konvention; sie geben den standardisierten vierten Moment gemäß der mathematischen Definition an. Dies ist auch als "nicht-exzessive" (oder "Pearson'sche") Kurtosis bekannt und hat für die Standardnormalverteilung den Wert 3.0.
stats.Normal().moment(4, kind='standardized')
np.float64(3.0)
Zur Bequemlichkeit bietet die Methode kurtosis ein Argument convention, um zwischen den beiden zu wählen.
stats.Normal().kurtosis(convention='excess'), stats.Normal().kurtosis(convention='non-excess')
(np.float64(0.0), np.float64(3.0))
Zufällsvariaten#
Die Methode rvs der alten Infrastruktur wurde durch sample ersetzt, aber es gibt zwei Unterschiede, die beachtet werden sollten, wenn entweder 1) die Kontrolle über den Zufallszustand erforderlich ist oder 2) Arrays für Form-, Orts- oder Skalenparameter verwendet werden.
Erstens wird das Argument random_state gemäß SPEC 7 durch rng ersetzt. Ein Muster zur Kontrolle des Zufallszustands war in der Vergangenheit die Verwendung von numpy.random.seed oder die Übergabe von ganzzahligen Seeds an das Argument random_state. Die ganzzahligen Seeds wurden in Instanzen von numpy.random.RandomState konvertiert, so dass das Verhalten für einen gegebenen ganzzahligen Seed in diesen beiden Fällen identisch wäre.
import numpy as np
np.random.seed(1)
dist = stats.norm
dist.rvs(), dist.rvs(random_state=1)
(np.float64(1.6243453636632417), np.float64(1.6243453636632417))
In der neuen Infrastruktur übergeben Sie Instanzen von numpy.Generator an das Argument rng von sample, um den Zufallszustand zu kontrollieren. Beachten Sie, dass ganzzahlige Seeds nun in Instanzen von numpy.random.Generator konvertiert werden, nicht in Instanzen von numpy.random.RandomState.
X = stats.Normal()
rng = np.random.default_rng(1) # instantiate a numpy.random.Generator
X.sample(rng=rng), X.sample(rng=1)
(np.float64(0.345584192064786), np.float64(0.345584192064786))
Zweitens ersetzt das Argument shape das Argument size.
dist.rvs(size=(3, 4))
array([[-0.61175641, -0.52817175, -1.07296862, 0.86540763],
[-2.3015387 , 1.74481176, -0.7612069 , 0.3190391 ],
[-0.24937038, 1.46210794, -2.06014071, -0.3224172 ]])
X.sample(shape=(3, 4))
array([[-0.31481026, 0.62016202, 0.30347577, 2.06372074],
[ 0.269438 , 0.45327138, 1.52273524, 0.42915731],
[-0.97010282, 0.33128361, -1.16448709, 0.47495506]])
Abgesehen vom Unterschied im Namen gibt es einen Unterschied im Verhalten, wenn Array-Formparameter beteiligt sind. Zuvor musste die Form der Verteilungsparameter-Arrays in size enthalten sein.
dist.rvs(size=(3, 4, 2), loc=[0, 1]).shape # `loc` has shape (2,)
(3, 4, 2)
Nun wird die Form der Parameter-Arrays als Eigenschaft des Zufallsvariablen-Objekts selbst betrachtet. Die Angabe der Form von Array-Formparametern wäre redundant und wird daher nicht bei der Angabe der shape der Stichprobe berücksichtigt.
Y = stats.Normal(mu = [0, 1])
Y.sample(shape=(3, 4)).shape # the sample has shape (3, 4); each element is of shape (2,)
(3, 4, 2)
Wahrscheinlichkeitsintervall (auch "Konfidenzintervall" genannt)#
Die alte Infrastruktur bot eine Methode interval, die standardmäßig ein symmetrisches (um den Median) Intervall zurückgab, das einen angegebenen Prozentsatz der Wahrscheinlichkeitsmasse der Verteilung enthielt.
a = 0.95
dist.interval(confidence=a)
(np.float64(-1.959963984540054), np.float64(1.959963984540054))
Rufen Sie nun die inversen CDF- und komplementären CDF-Methoden mit der gewünschten Wahrscheinlichkeitsmasse in jedem Schwanz auf.
p = 1 - a
X.icdf(p/2), X.iccdf(p/2)
(np.float64(-1.959963984540054), np.float64(1.959963984540054))
Likelihood-Funktion#
Die alte Infrastruktur bietet eine Funktion zur Berechnung der **n**egativen **l**og-**l**ikelihood-**F**unktion, fälschlicherweise benannt nnlf (statt nllf). Sie akzeptiert die Parameter der Verteilung als Tupel und Beobachtungen als Array.
mu = 0
sigma = 1
data = stats.norm.rvs(size=100, loc=mu, scale=sigma)
stats.norm.nnlf((mu, sigma), data)
np.float64(131.07116392314364)
Berechnen Sie nun einfach die negative Log-Likelihood gemäß ihrer mathematischen Definition.
X = stats.Normal(mu=mu, sigma=sigma)
-X.logpdf(data).sum()
np.float64(131.07116392314364)
Erwartungswerte#
Die Methode expect der alten Infrastruktur schätzt ein bestimmtes Integral einer beliebigen Funktion, gewichtet mit der PDF der Verteilung. Zum Beispiel ist der vierte Moment der Verteilung gegeben durch
def f(x): return x**4
stats.norm.expect(f, lb=-np.inf, ub=np.inf)
np.float64(3.000000000000001)
Dies bietet wenig zusätzlichen Komfort gegenüber dem, was der Quellcode leistet: die numerische Integration mit scipy.integrate.quad.
from scipy import integrate
def f(x): return x**4 * stats.norm.pdf(x)
integrate.quad(f, a=-np.inf, b=np.inf) # integral estimate, estimate of the error
(3.0000000000000053, 1.2043244026618655e-08)
Natürlich kann dies genauso einfach mit der neuen Infrastruktur erfolgen.
def f(x): return x**4 * X.pdf(x)
integrate.quad(f, a=-np.inf, b=np.inf) # integral estimate, estimate of the error
(3.0000000000000053, 1.2043244043338238e-08)
Das Argument conditional skaliert das Ergebnis einfach mit dem Kehrwert der Wahrscheinlichkeitsmasse, die innerhalb des Intervalls enthalten ist.
a, b = -1, 3
def f(x): return x**4
stats.norm.expect(f, lb=a, ub=b, conditional=True)
np.float64(1.657813862143119)
Durch direkte Verwendung von quad, also
def f(x): return x**4 * stats.norm.pdf(x)
prob = stats.norm.cdf(b) - stats.norm.cdf(a)
integrate.quad(f, a=a, b=b)[0] / prob
np.float64(1.6578138621431193)
Und mit den neuen Zufallsvariablen
integrate.quad(f, a=a, b=b)[0] / X.cdf(a, b)
np.float64(1.6578138621431193)
Beachten Sie, dass die Methode cdf der neuen Zufallsvariablen zwei Argumente akzeptiert, um die Wahrscheinlichkeitsmasse innerhalb des angegebenen Intervalls zu berechnen. In vielen Fällen kann dies Subtraktionsfehler ("katastrophale Auslöschung") vermeiden, wenn die Wahrscheinlichkeitsmasse sehr klein ist.
Anpassung (Fitting)#
Orts- / Skalen-Schätzung#
Die alte Infrastruktur bot eine Funktion zur Schätzung von Orts- und Skalenparametern der Verteilung aus Daten.
rng = np.random.default_rng(91392794601852341588152500276639671056)
dist = stats.weibull_min
c, loc, scale = 0.5, 0, 4.
data = dist.rvs(size=100, c=c, loc=loc, scale=scale, random_state=rng)
dist.fit_loc_scale(data, c)
# compare against 0 (default location) and 4 (specified scale)
(np.float64(1.8268432669973347), np.float64(1.9640905288934327))
Basierend auf dem Quellcode lässt sich die Methode leicht nachbilden.
X = Weibull(c=c)
def fit_loc_scale(X, data):
m, v = X.mean(), X.variance()
m_, v_ = data.mean(), data.var()
scale = np.sqrt(v_ / v)
loc = m_ - scale*m
return loc, scale
fit_loc_scale(X, data)
(np.float64(1.8268432669973347), np.float64(1.9640905288934327))
Beachten Sie, dass die Schätzungen in diesem Beispiel recht schlecht sind und die schlechte Leistung der Heuristik in die Entscheidung einfloss, keinen Ersatz anzubieten.
Maximum-Likelihood-Schätzung#
Die letzte Methode der alten Infrastruktur ist fit, die die Orts-, Skalen- und Formparameter einer zugrundeliegenden Verteilung aus einer Stichprobe der Verteilung schätzt.
c_, loc_, scale_ = stats.weibull_min.fit(data)
c_, loc_, scale_
(np.float64(0.5960699537061247),
np.float64(1.8950104942593064e-05),
np.float64(4.015875612107546))
Der Komfort dieser Methode ist Segen und Fluch zugleich.
Wenn es funktioniert, wird die Einfachheit sehr geschätzt. Für einige Verteilungen wurden analytische Ausdrücke für die Maximum-Likelihood-Schätzungen (MLE) der Parameter manuell programmiert, und für diese Verteilungen ist die Methode fit recht zuverlässig.
Für die meisten Verteilungen wird die Anpassung jedoch durch numerische Minimierung der negativen Log-Likelihood-Funktion durchgeführt. Dies ist nicht garantiert erfolgreich – sowohl wegen inhärenter Einschränkungen der MLE als auch des Standes der Technik der numerischen Optimierung –, und in diesen Fällen ist der Benutzer von fit gefangen. Ein gewisses Verständnis hilft jedoch, den Erfolg sicherzustellen, daher präsentieren wir hier ein Mini-Tutorial zum Anpassen mit der neuen Infrastruktur.
Zunächst sei darauf hingewiesen, dass MLE eine von mehreren möglichen Strategien zum Anpassen von Verteilungen an Daten ist. Sie tut nichts weiter, als die Werte der Verteilungsparameter zu finden, für die die negative Log-Likelihood (NLLF) minimiert wird. Beachten Sie, dass für die Verteilung, aus der die Daten generiert wurden, die NLLF ist
stats.weibull_min.nnlf((c, loc, scale), data)
np.float64(246.9503871545133)
Die NLLF der mit fit geschätzten Parameter sind niedriger
stats.weibull_min.nnlf((c_, loc_, scale_), data)
np.float64(230.35385152369787)
Daher betrachtet fit seine Arbeit als erledigt, unabhängig davon, ob dies den Vorstellungen des Benutzers von einem "guten Fit" entspricht oder ob die Parameter innerhalb angemessener Grenzen liegen. Abgesehen davon, dass dem Benutzer die Angabe einer Vermutung für die Verteilungsparameter gestattet wird, bietet es wenig Kontrolle über den Prozess. ( *Hinweis: Technisch gesehen kann das Argument optimizer für mehr Kontrolle verwendet werden, aber dies ist nicht gut dokumentiert und seine Verwendung hebt jeglichen Komfort auf, den die Methode fit bietet.*)
Ein weiteres Problem ist, dass MLE für einige Verteilungen von Natur aus schlecht verhält. In diesem Beispiel können wir beispielsweise die NLLF beliebig niedrig machen, indem wir einfach den Ort auf das Minimum der Daten setzen – selbst für unsinnige Werte der Form- und Skalenparameter.
stats.weibull_min.nnlf((0.1, np.min(data), 10), data)
np.float64(-inf)
Zusätzlich zu diesen Problemen schätzt fit standardmäßig alle Verteilungsparameter, einschließlich des Ortes. Im obigen Beispiel sind wir wahrscheinlich nur an der gebräuchlicheren zweiparametrigen Weibull-Verteilung interessiert, da der tatsächliche Ort Null ist. fit *kann* dies berücksichtigen, indem angegeben wird, dass der Ort ein fester Parameter ist.
# c_, loc_, scale_ = stats.weibull_min.fit(data, loc=0) # careful! this provides loc=0 as a *guess*
c_, loc_, scale_ = stats.weibull_min.fit(data, floc=0)
c_, loc_, scale_
(np.float64(0.5834128280886433), 0, np.float64(3.829972848420729))
stats.weibull_min.nnlf((c_, loc_, scale_), data)
np.float64(244.9617429249505)
Aber durch die Bereitstellung einer fit-Methode, die angeblich "einfach funktioniert", werden Benutzer ermutigt, einige dieser wichtigen Details zu vernachlässigen.
Stattdessen schlagen wir vor, dass es fast genauso einfach ist, Verteilungen mit den generischen Optimierungswerkzeugen von SciPy an Daten anzupassen. Dies ermöglicht es dem Benutzer jedoch, die Anpassung gemäß seiner bevorzugten Zielfunktion durchzuführen, bietet Optionen, wenn die Dinge nicht wie erwartet funktionieren, und hilft dem Benutzer, die häufigsten Fallstricke zu vermeiden.
Nehmen wir zum Beispiel an, unsere gewünschte Zielfunktion ist tatsächlich die negative Log-Likelihood. Sie ist einfach als Funktion des Formparameters c und nur des Skalen zu definieren, wobei der Ort bei seinem Standardwert von Null belassen wird.
def nllf(x):
c, scale = x # pass (only) `c` and `scale` as elements of `x`
X = Weibull(c=c) * scale
return -X.logpdf(data).sum()
nllf((c_, scale_))
np.float64(244.96174292495053)
Um die Minimierung durchzuführen, können wir scipy.optimize.minimize verwenden.
from scipy import optimize
eps = 1e-10 # numerical tolerance to avoid invalid parameters
lb = [eps, eps] # lower bound on `c` and `scale`
ub = [10, 10] # upper bound on `c` and `scale`
x0 = [1, 1] # guess to get optimization started
bounds = optimize.Bounds(lb, ub)
res_mle = optimize.minimize(nllf, x0, bounds=bounds)
res_mle
message: CONVERGENCE: NORM OF PROJECTED GRADIENT <= PGTOL
success: True
status: 0
fun: 244.96174292277675
x: [ 5.834e-01 3.830e+00]
nit: 13
jac: [ 5.684e-06 0.000e+00]
nfev: 45
njev: 15
hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
Der Wert der Zielfunktion ist im Wesentlichen identisch, und die PDFs sind nicht zu unterscheiden.
import matplotlib.pyplot as plt
x = np.linspace(eps, 15, 300)
c_, scale_ = res_mle.x
X = Weibull(c=c_)*scale_
plt.plot(x, X.pdf(x), '-', label='numerical optimization')
c_, _, scale_ = stats.weibull_min.fit(data, floc=0)
Y = Weibull(c=c_)*scale_
plt.plot(x, Y.pdf(x), '--', label='`weibull_min.fit`')
plt.hist(data, bins=np.linspace(0, 20, 30), density=True, alpha=0.1)
plt.xlabel('x')
plt.ylabel('pdf(x)')
plt.legend()
plt.ylim(0, 0.5)
plt.show()
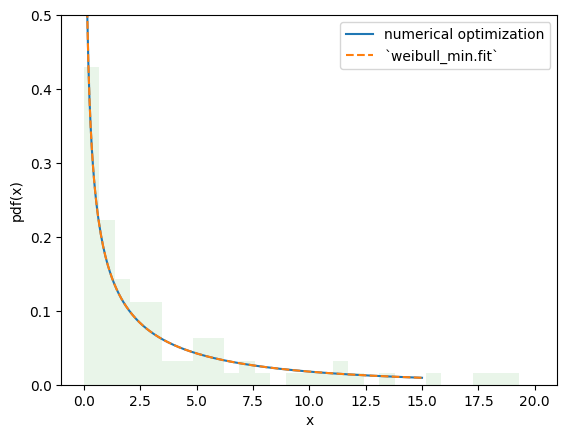
Mit diesem Ansatz ist es jedoch trivial, Änderungen am Anpassungsverfahren vorzunehmen, um unseren Bedürfnissen gerecht zu werden, und ermöglicht Schätzverfahren, die über die von rv_continuous.fit bereitgestellten hinausgehen. Zum Beispiel können wir Maximum Spacing Estimation (MSE) durchführen, indem wir die Zielfunktion auf das **n**egative **l**og **p**roduct **s**pacing wie folgt ändern.
def nlps(x):
c, scale = x
X = Weibull(c=c) * scale
x = np.sort(np.concatenate((data, X.support()))) # Append the endpoints of the support to the data
return -X.logcdf(x[:-1], x[1:]).sum().real # Minimize the sum of the logs the probability mass between points
res_mps = optimize.minimize(nlps, x0, bounds=bounds)
res_mps.x
array([0.5591792 , 3.85552363])
Für die Methode der L-Momente (die versucht, die Verteilungs- und Stichproben-L-Momente abzugleichen)
def lmoment_residual(x):
c, scale = x
X = Weibull(c=c) * scale
E11 = stats.order_statistic(X, r=1, n=1).mean()
E12, E22 = stats.order_statistic(X, r=[1, 2], n=2).mean()
lmoments_X = [E11, 0.5*(E22 - E12)] # the first two l-moments of the distribution
lmoments_x = stats.lmoment(data, order=[1, 2]) # first two l-moments of the data
return np.linalg.norm(lmoments_x - lmoments_X) # Minimize the norm of the difference
x0 = [0.4, 3] # This method is a bit sensitive to the initial guess
res_lmom = optimize.minimize(lmoment_residual, x0, bounds=bounds)
res_lmom.x, res_lmom.fun # residual should be ~0
(array([0.60943275, 3.90234501]), np.float64(5.041000173121575e-07))
Die Plots für alle drei Methoden sehen ähnlich aus und scheinen die Daten zu beschreiben, was uns ein gewisses Vertrauen gibt, dass wir eine gute Anpassung erzielt haben.
import matplotlib.pyplot as plt
x = np.linspace(eps, 10, 300)
for res, label in [(res_mle, "MLE"), (res_mps, "MPS"), (res_lmom, "L-moments")]:
c_, scale_ = res.x
X = Weibull(c=c_)*scale_
plt.plot(x, X.pdf(x), '-', label=label)
plt.hist(data, bins=np.linspace(0, 10, 30), density=True, alpha=0.1)
plt.xlabel('x')
plt.ylabel('pdf(x)')
plt.legend()
plt.ylim(0, 0.3)
plt.show()
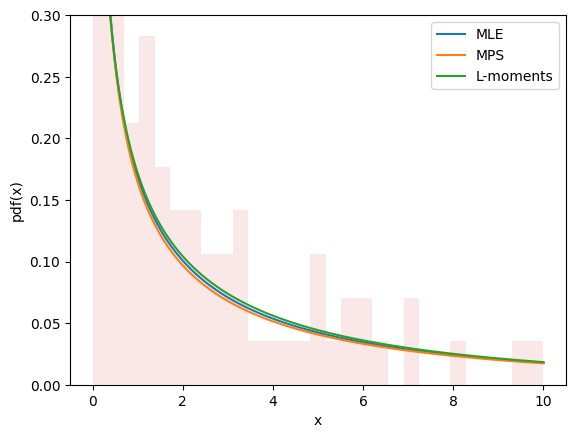
Schätzung beinhaltet nicht immer die Anpassung von Verteilungen an Daten. Zum Beispiel musste in gh-12134 ein Benutzer die Form- und Skalenparameter der Weibull-Verteilung berechnen, um einen gegebenen Mittelwert und eine Standardabweichung zu erreichen. Dies passt leicht in den gleichen Rahmen.
moments_0 = np.asarray([8, 20]) # desired mean and standard deviation
def f(x):
c, scale = x
X = Weibull(c=c) * scale
moments_X = X.mean(), X.standard_deviation()
return np.linalg.norm(moments_X - moments_0)
bounds.lb = np.asarray([0.1, 0.1]) # the Weibull distribution is problematic for very small c
res = optimize.minimize(f, x0, bounds=bounds, method='slsqp') # easily change the minimization method
res
message: Optimization terminated successfully
success: True
status: 0
fun: 4.594829312984325e-07
x: [ 4.627e-01 3.430e+00]
nit: 21
jac: [ 1.322e+02 -2.330e-01]
nfev: 100
njev: 21
multipliers: []
Neue und erweiterte Funktionen#
Transformationen#
Mathematische Transformationen können auf Zufallsvariablen angewendet werden. Zum Beispiel funktionieren viele elementare arithmetische Operationen (+, -, *, /, **) zwischen Zufallsvariablen und Skalaren.
Zum Beispiel können wir sehen, dass der Kehrwert einer Weibull-verteilten RV gemäß scipy.stats.invweibull verteilt ist. (Eine "inverse" Verteilung ist typischerweise die zugrundeliegende Verteilung des Kehrwerts einer Zufallsvariablen.)
c = 10.6
X = Weibull(c=10.6)
Y = 1 / X # compare to `invweibull`
Y.plot()
x = np.linspace(0.8, 2.05, 300)
plt.plot(x, stats.invweibull(c=c).pdf(x), '--')
plt.legend(['`1 / X`', '`invweibull`'])
plt.title("Inverse Weibull PDF")
plt.show()
/home/treddy/github_projects/scipy/doc/build/env/lib/python3.11/site-packages/scipy/stats/_distribution_infrastructure.py:1966: RuntimeWarning: divide by zero encountered in divide
h=lambda u: 1 / u, dh=lambda u: 1 / u ** 2)
/home/treddy/github_projects/scipy/doc/build/env/lib/python3.11/site-packages/scipy/stats/_continuous_distns.py:2747: RuntimeWarning: invalid value encountered in multiply
return c*pow(x, c-1)*np.exp(-pow(x, c))
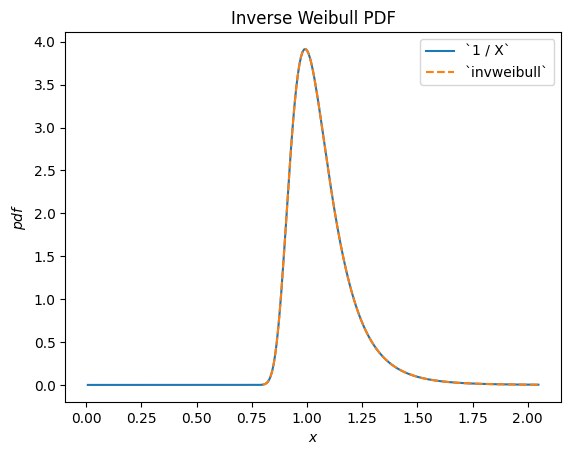
scipy.stats.chi2 beschreibt die Summe der Quadrate von normalverteilten Zufallsvariablen.
X = stats.Normal()
Y = X**2 # compare to chi2
Y.plot(t=('x', eps, 5));
x = np.linspace(eps, 5, 300)
plt.plot(x, stats.chi2(df=1).pdf(x), '--')
plt.ylim(0, 3)
plt.legend(['`X**2`', '`chi2`'])
plt.title("Chi-squared PDF")
plt.show()
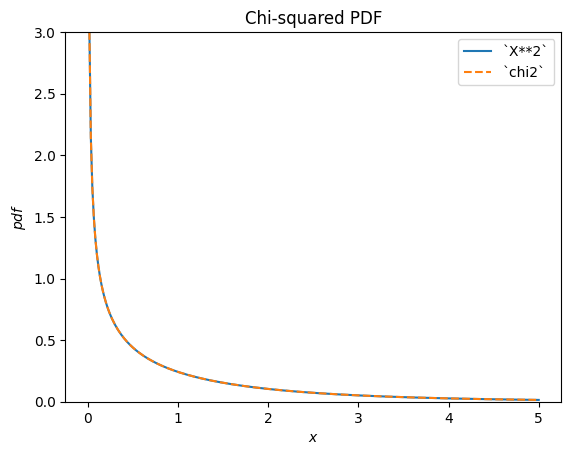
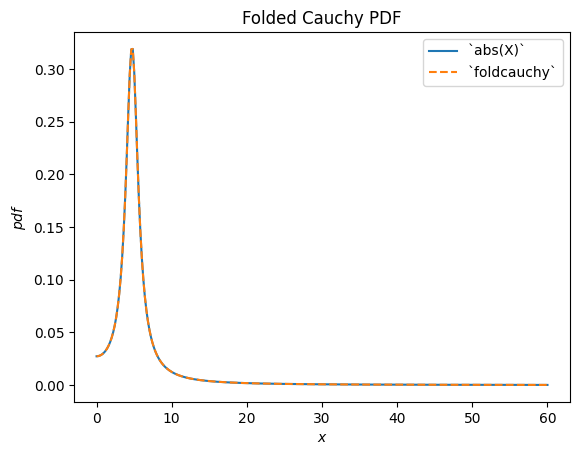
scipy.stats.foldcauchy beschreibt den Absolutbetrag einer Cauchy-verteilten Zufallsvariablen. (Eine "gefaltete" Verteilung ist die zugrundeliegende Verteilung des Absolutbetrags einer Zufallsvariablen.)
Cauchy = stats.make_distribution(stats.cauchy)
c = 4.72
X = Cauchy() + c
Y = abs(X) # compare to `foldcauchy`
Y.plot(t=('x', 0, 60))
x = np.linspace(0, 60, 300)
plt.plot(x, stats.foldcauchy(c=c).pdf(x), '--')
plt.legend(['`abs(X)`', '`foldcauchy`'])
plt.title("Folded Cauchy PDF")
plt.show()
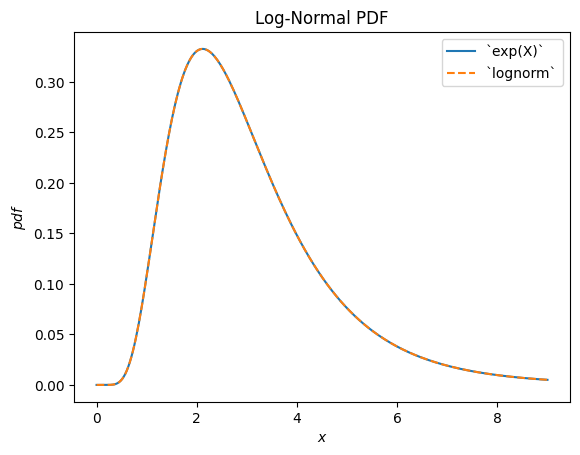
scipy.stats.lognormal beschreibt die Exponentialfunktion einer normalverteilten Zufallsvariablen. Sie ist so benannt, weil der Logarithmus der resultierenden Zufallsvariablen normalverteilt ist. (Im Allgemeinen ist eine "Log"-Verteilung typischerweise die zugrundeliegende Verteilung der *Exponentialfunktion* einer Zufallsvariablen.)
u, s = 1, 0.5
X = stats.Normal()*s + u
Y = stats.exp(X) # compare to `lognorm`
Y.plot(t=('x', eps, 9))
x = np.linspace(eps, 9, 300)
plt.plot(x, stats.lognorm(s=s, scale=np.exp(u)).pdf(x), '--')
plt.legend(['`exp(X)`', '`lognorm`'])
plt.title("Log-Normal PDF")
plt.show()
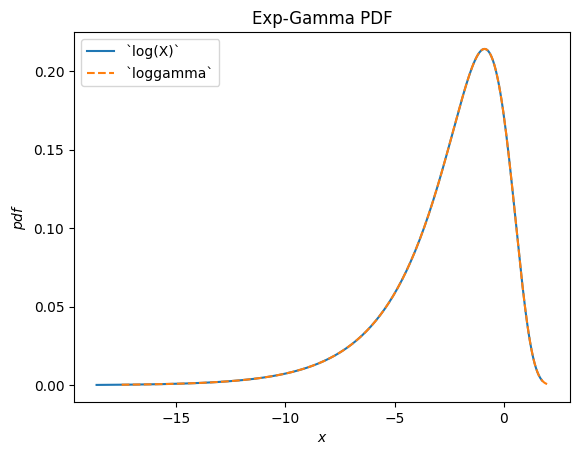
scipy.stats.loggamma beschreibt den Logarithmus einer Gamma-verteilten Zufallsvariablen. Beachten Sie, dass gemäß typischer Konventionen der passende Name dieser Verteilung Exp-Gamma wäre, da die Exponentialfunktion der RV Gamma-verteilt ist.
Gamma = stats.make_distribution(stats.gamma)
a = 0.414
X = Gamma(a=a)
Y = stats.log(X) # compare to `loggamma`
Y.plot()
x = np.linspace(-17.5, 2, 300)
plt.plot(x, stats.loggamma(c=a).pdf(x), '--')
plt.legend(['`log(X)`', '`loggamma`'])
plt.title("Exp-Gamma PDF")
plt.show()
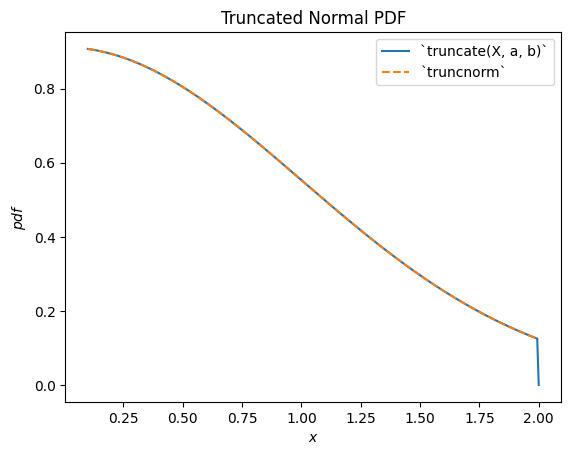
scipy.stats.truncnorm ist die zugrundeliegende Verteilung einer abgeschnittenen normalen Zufallsvariablen. Beachten Sie, dass die Trunkations-Transformation entweder vor oder nach dem Verschieben und Skalieren der normalverteilten Zufallsvariablen angewendet werden kann, was es viel einfacher machen kann, das gewünschte Ergebnis als mit scipy.stats.truncnorm (das inhärent *nach* der Trunkation verschiebt und skaliert) zu erzielen.
a, b = 0.1, 2
X = stats.Normal()
Y = stats.truncate(X, a, b) # compare to `truncnorm`
Y.plot()
x = np.linspace(a, b, 300)
plt.plot(x, stats.truncnorm(a, b).pdf(x), '--')
plt.legend(['`truncate(X, a, b)`', '`truncnorm`'])
plt.title("Truncated Normal PDF")
plt.show()
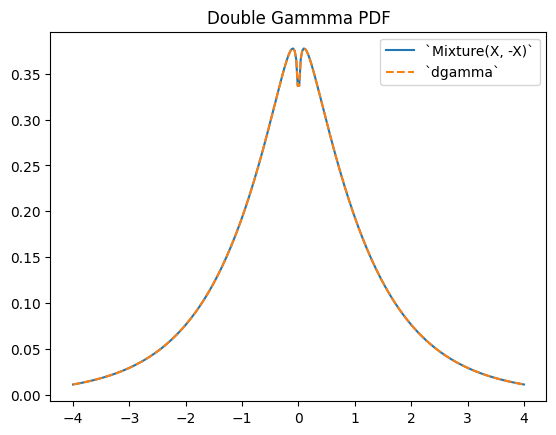
scipy.stats.dgamma ist eine Mischung aus zwei Gamma-verteilten RVs, von denen eine um den Ursprung gespiegelt ist. (Typischerweise ist eine "doppelte" Verteilung die zugrundeliegende Verteilung einer Mischung von RVs, von denen eine gespiegelt ist.)
a = 1.1
X = Gamma(a=a)
Y = stats.Mixture((X, -X), weights=[0.5, 0.5])
# plot method not available for mixtures
x = np.linspace(-4, 4, 300)
plt.plot(x, Y.pdf(x))
plt.plot(x, stats.dgamma(a=a).pdf(x), '--')
plt.legend(['`Mixture(X, -X)`', '`dgamma`'])
plt.title("Double Gammma PDF")
plt.show()
Einschränkungen#
Während die meisten arithmetischen Transformationen zwischen Zufallsvariablen und Python-Skalaren oder NumPy-Arrays unterstützt werden, gibt es einige Einschränkungen.
Das Potenzieren einer Zufallsvariablen mit einem Argument ist nur implementiert, wenn das Argument eine positive ganze Zahl ist.
Das Potenzieren eines Arguments mit einer Zufallsvariablen ist nur implementiert, wenn das Argument ein positives Skalar ungleich 1 ist.
Division durch eine Zufallsvariable ist nur implementiert, wenn die Unterstützung entweder ausschließlich nicht-negativ oder nicht-positiv ist.
Der Logarithmus einer Zufallsvariablen ist nur implementiert, wenn die Unterstützung nicht-negativ ist. (Der Logarithmus negativer Werte ist imaginär.)
Arithmetische Operationen zwischen zwei Zufallsvariablen werden *noch nicht* unterstützt. Beachten Sie, dass solche Operationen mathematisch viel komplexer sind; beispielsweise beinhaltet die PDF der Summe zweier Zufallsvariablen die Faltung der beiden PDFs.
Außerdem, obwohl Transformationen komponierbar sind, können a) Trunkation und b) Verschiebung/Skalierung jeweils nur einmal durchgeführt werden. Zum Beispiel wird Y = 2 * stats.exp(X + 1) einen Fehler auslösen, da dies eine Verschiebung vor der Exponentialfunktion und eine Skalierung nach der Exponentialfunktion erfordern würde; dies wird als "zweimaliges Verschieben/Skalieren" behandelt. Eine mathematische Vereinfachung ist hier jedoch möglich (und in vielen Fällen), um das Problem zu vermeiden: Y = (2*math.exp(2)) * stats.exp(X) ist äquivalent und erfordert nur eine Skalierungsoperation.
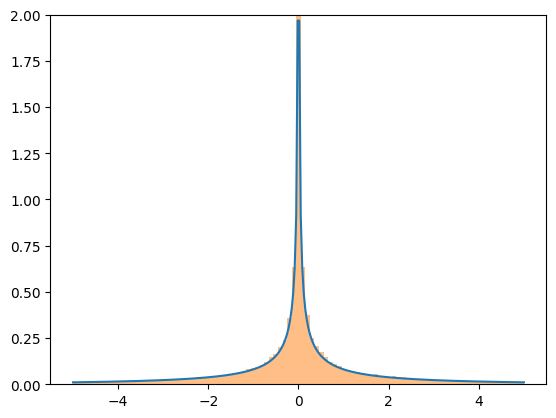
Obwohl die Transformationen recht robust sind, basieren sie alle auf generischen Implementierungen, die numerische Schwierigkeiten verursachen können. Wenn Sie sich Sorgen über die Genauigkeit der Ergebnisse einer Transformation machen, sollten Sie die resultierende PDF mit einem Histogramm einer Zufallsstichprobe vergleichen.
X = stats.Normal()
Y = X**3
x = np.linspace(-5, 5, 300)
plt.plot(x, Y.pdf(x), label='pdf')
plt.hist(X.sample(100000)**3, density=True, bins=np.linspace(-5, 5, 100), alpha=0.5);
plt.ylim(0, 2)
plt.show()
Quasi-Monte-Carlo-Stichprobenziehung#
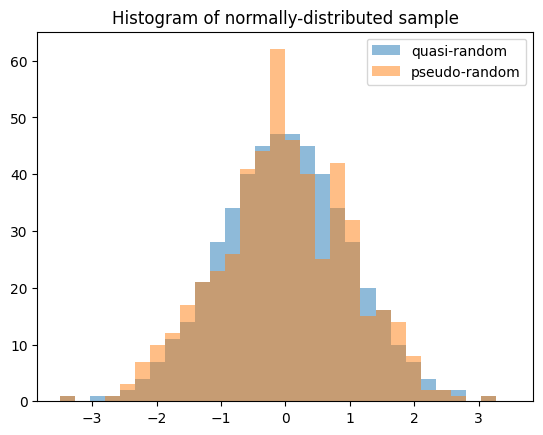
Zufallsvariablen ermöglichen die Erzeugung von quasi-zufälligen Stichproben mit geringer Diskrepanz aus statistischen Verteilungen.
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
X = stats.Normal()
rng = np.random.default_rng(7824387278234)
qrng = stats.qmc.Sobol(1, rng=rng) # instantiate a QMCEngine
bins = np.linspace(-3.5, 3.5, 31)
plt.hist(X.sample(512, rng=qrng), bins, alpha=0.5, label='quasi-random')
plt.hist(X.sample(512, rng=rng), bins, alpha=0.5, label='pseudo-random')
plt.title('Histogram of normally-distributed sample')
plt.legend()
plt.show()
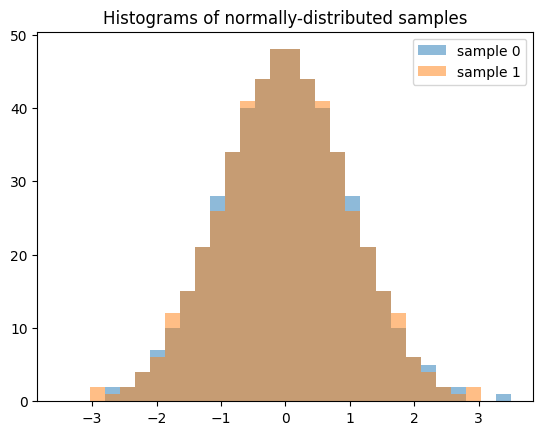
Beachten Sie, dass bei der Erzeugung mehrerer Stichproben (z. B. len(shape) > 1) jeder Slice entlang der nullten Achse eine unabhängige Sequenz mit geringer Diskrepanz ist. Das Folgende erzeugt zwei unabhängige QMC-Stichproben mit jeweils 512 Elementen.
samples = X.sample((512, 2), rng=qrng)
plt.hist(samples[:, 0], bins, alpha=0.5, label='sample 0')
plt.hist(samples[:, 1], bins, alpha=0.5, label='sample 1')
plt.title('Histograms of normally-distributed samples')
plt.legend()
plt.show()
Das Ergebnis unterscheidet sich erheblich, wenn wir 512 unabhängige QMC-Sequenzen mit jeweils 2 Elementen erzeugen.
samples = X.sample((2, 512), rng=qrng)
plt.hist(samples[0], bins, alpha=0.5, label='sample 0')
plt.hist(samples[1], bins, alpha=0.5, label='sample 1')
plt.title('Histograms of normally-distributed samples')
plt.legend()
plt.show()
Genauigkeit#
Bei einigen Verteilungen, wie scipy.stats.norm, sind fast alle Methoden der Verteilung für eine genaue Berechnung optimiert. Bei anderen, wie scipy.stats.gausshyper, ist wenig mehr als die PDF definiert, und die anderen Methoden müssen numerisch basierend auf der PDF berechnet werden. Zum Beispiel wird die Überlebensfunktion (komplementäre CDF) der Gauss-hypergeometrischen Verteilung berechnet, indem die PDF von 0 (dem linken Ende der Unterstützung) bis x numerisch integriert wird, um die CDF zu erhalten, dann wird das Komplement gebildet.
a, b, c, z = 1.5, 2.5, 2, 0
x = 0.5
frozen = stats.gausshyper(a=a, b=b, c=c, z=z)
frozen.sf(x)
np.float64(0.28779340921080643)
frozen.sf(x) == 1 - integrate.quad(frozen.pdf, 0, x)[0]
np.True_
Ein anderer Ansatz wäre jedoch, die PDF von x bis 1 (dem rechten Ende der Unterstützung) numerisch zu integrieren.
integrate.quad(frozen.pdf, x, 1)[0]
0.28779340919669805
Dies sind unterschiedliche, aber gleichermaßen gültige Ansätze. Wenn also angenommen wird, dass die PDF genau ist, ist es unwahrscheinlich, dass die beiden Ergebnisse auf die gleiche Weise ungenau sind. Daher können wir die Genauigkeit der Ergebnisse schätzen, indem wir sie vergleichen.
res1 = frozen.sf(x)
res2 = integrate.quad(frozen.pdf, x, 1)[0]
abs((res1 - res2) / res1)
np.float64(4.902259981810363e-11)
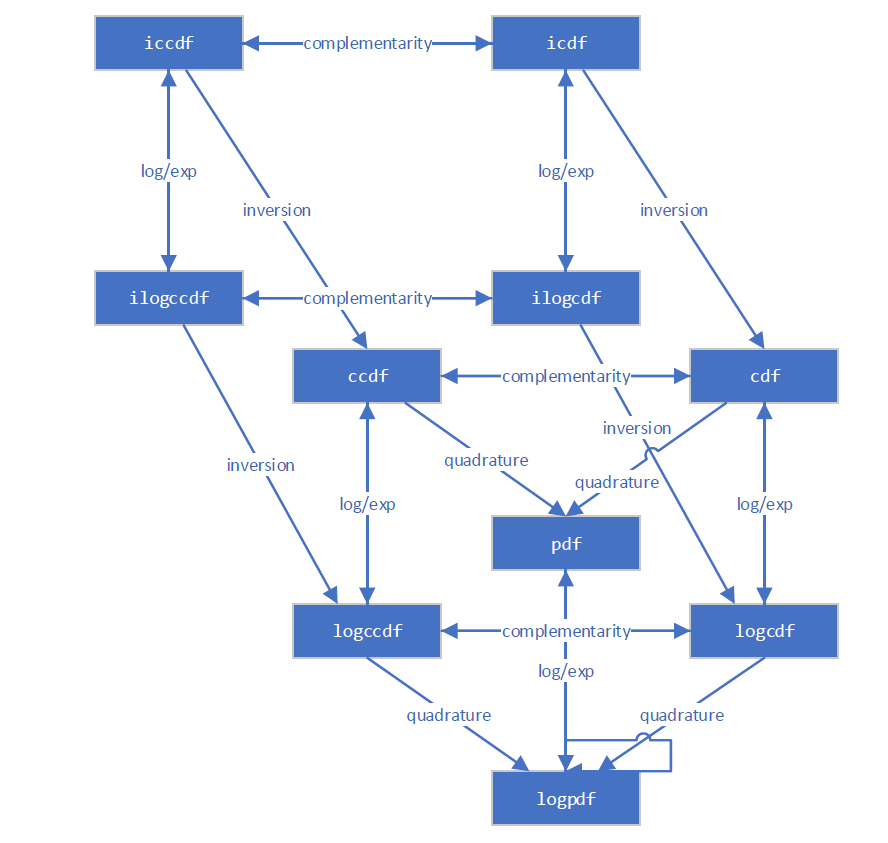
Die neue Infrastruktur kennt mehrere verschiedene Wege zur Berechnung der meisten Größen. Dieses Diagramm veranschaulicht beispielsweise die Beziehungen zwischen verschiedenen Verteilungsfunktionen.
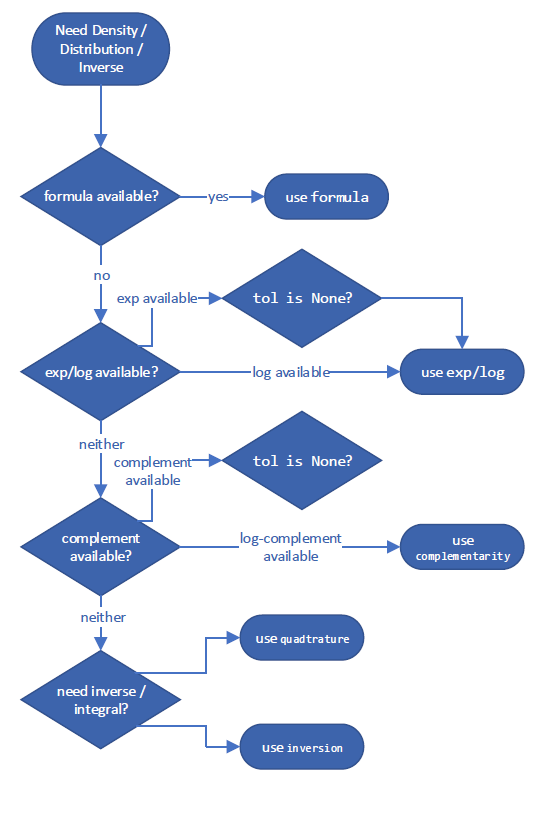
Es folgt eine Entscheidungsbaum, um die Methode auszuwählen, die voraussichtlich die genaueste Schätzung der Größe liefert. Diese spezifischen Entscheidungsbäume für die "beste" Methode können zwischen SciPy-Versionen variieren, aber ein Beispiel für die Berechnung der komplementären CDF könnte wie folgt aussehen:
und zur Berechnung eines Moments
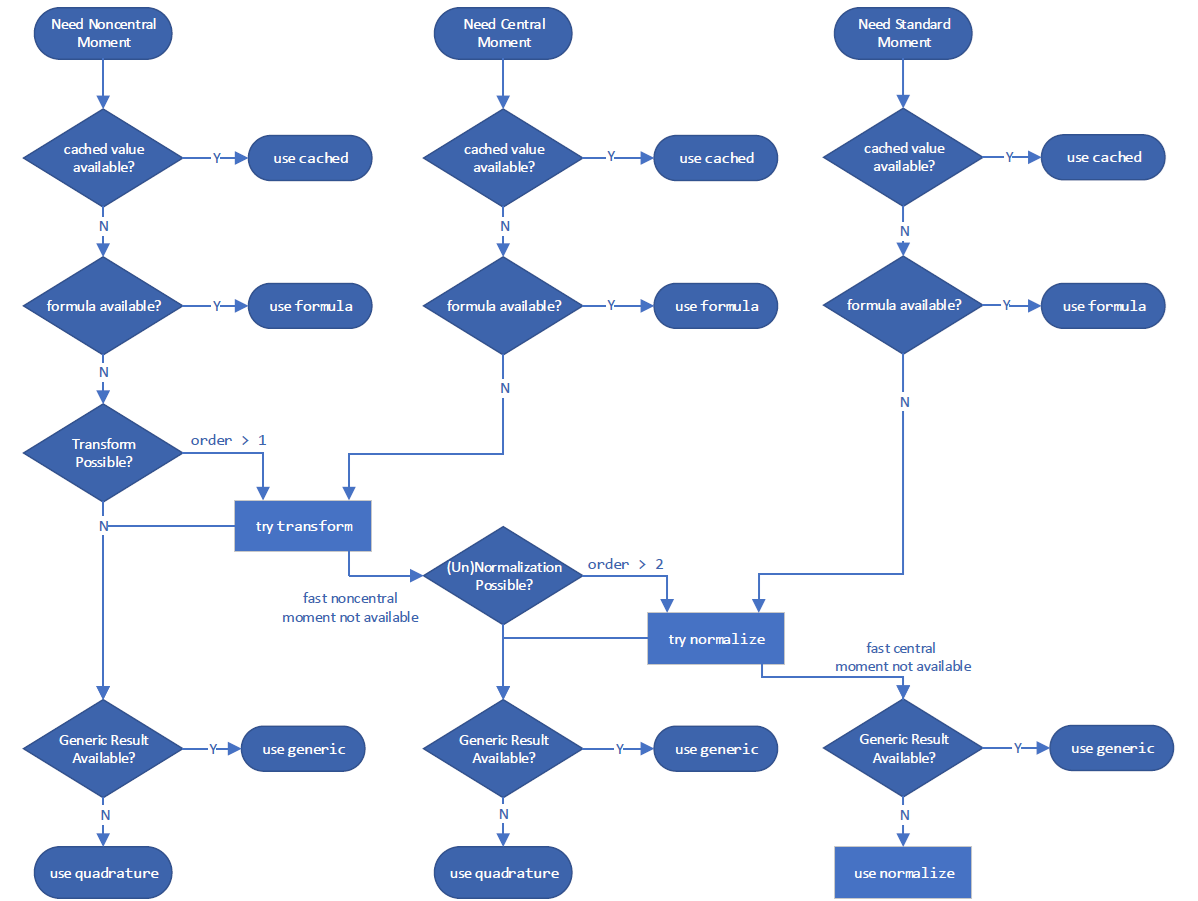
Sie können jedoch die verwendete Methode mit dem Argument method überschreiben.
GaussHyper = stats.make_distribution(stats.gausshyper)
X = GaussHyper(a=a, b=b, c=c, z=z)
Für ccdf integriert method='quadrature' die PDF im rechten Schwanz.
X.ccdf(x, method='quadrature') == integrate.tanhsinh(X.pdf, x, 1).integral
np.True_
method='complement' bildet das Komplement der CDF.
X.ccdf(x, method='complement') == (1 - integrate.tanhsinh(X.pdf, 0, x).integral)
np.True_
method='logexp' nimmt die Exponentialfunktion des Logarithmus der CCDF.
X.ccdf(x, method='logexp') == np.exp(integrate.tanhsinh(lambda x: X.logpdf(x), x, 1, log=True).integral)
np.True_
Im Zweifelsfall sollten Sie versuchen, verschiedene methods auszuprobieren, um eine bestimmte Größe zu berechnen.
Leistung#
Betrachten Sie die Leistung von Berechnungen mit der Gauss-hypergeometrischen Verteilung. Für skalare Formen und Argumente ist die Leistung der neuen und alten Infrastrukturen vergleichbar. Die neue Infrastruktur wird voraussichtlich nicht viel schneller sein; obwohl sie den "Overhead" der Parametervalidierung reduziert, ist sie bei der numerischen Integration von Skalargrößen nicht signifikant schneller, und letztere dominiert hier die Ausführungszeit.
%timeit X.cdf(x) # new infrastructure
439 μs ± 26.2 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
%timeit stats.gausshyper.cdf(x, a, b, c, z) # old infrastructure
346 μs ± 1.3 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
np.isclose(X.cdf(x), stats.gausshyper.cdf(x, a, b, c, z))
np.True_
Die neue Infrastruktur ist jedoch wesentlich schneller, wenn Arrays involviert sind. Dies liegt daran, dass der zugrundeliegende Integrator (scipy.integrate.tanhsinh) und der Wurzelzieher (scipy.optimize.elementwise.find_root), die für die neue Infrastruktur entwickelt wurden, nativ vektorisiert sind, während die Legacy-Routinen, die von der alten Infrastruktur verwendet werden (scipy.integrate.quad und scipy.optimize.brentq), dies nicht sind.
x = np.linspace(0, 1, 1000)
%timeit X.cdf(x) # new infrastructure
2.36 ms ± 1.25 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
%timeit stats.gausshyper.cdf(x, a, b, c, z) # old infrastructure
303 ms ± 70 μs per loop (mean ± std. dev. of 7 runs, 1 loop each)
Vergleichbare Leistungssteigerungen sind für Array-Berechnungen zu erwarten, wann immer die zugrundeliegenden Funktionen durch numerische Quadratur oder Inversion (Wurzelfindung) berechnet werden.
Visualisierung#
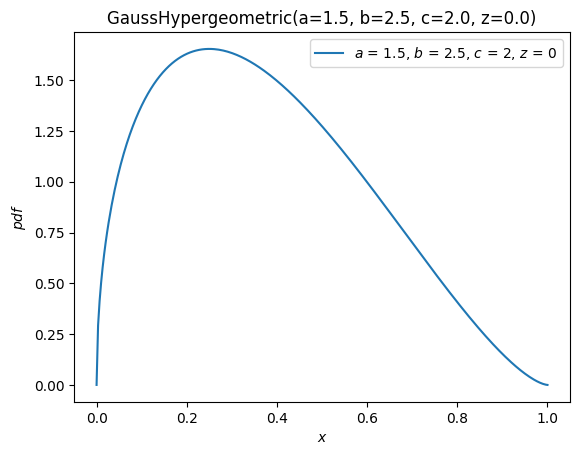
Wir können Funktionen der zugrundeliegenden Verteilung von Zufallsvariablen leicht mit der Komfortmethode plot visualisieren.
import matplotlib.pyplot as plt
ax = X.plot()
plt.show()
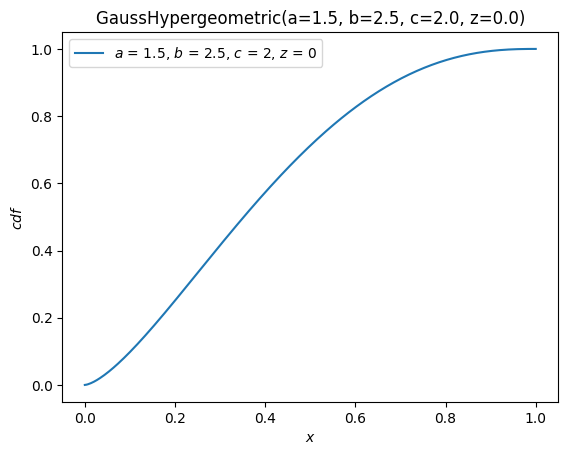
X.plot(y='cdf')
plt.show()
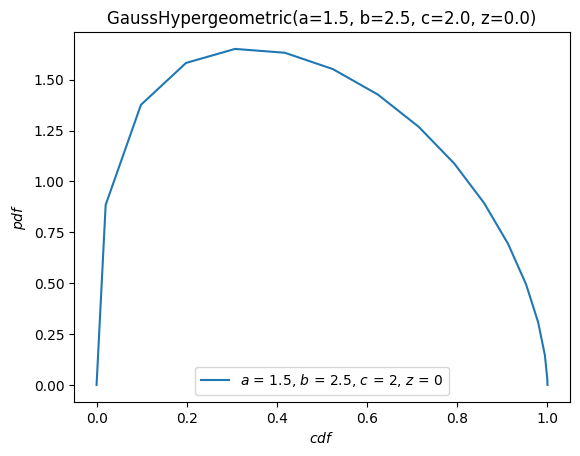
Die plot-Methode ist ziemlich flexibel und hat eine Signatur, die von The Grammar of Graphics inspiriert ist. Zum Beispiel mit dem Argument \(x\) auf \([-10, 10]\) die PDF gegen die CDF plotten.
X.plot('cdf', 'pdf', t=('x', -10, 10))
plt.show()
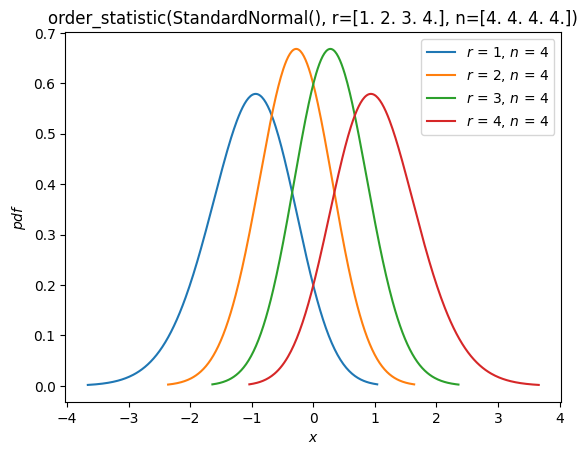
Ordnungsstatistiken#
Wie im Abschnitt "Fit" oben zu sehen ist, gibt es nun Unterstützung für die Verteilungen von Ordnungsstatistiken von Zufallsstichproben aus einer Verteilung. Zum Beispiel können wir die Wahrscheinlichkeitsdichtefunktionen der Ordnungsstatistiken einer Normalverteilung mit Stichprobengröße 4 plotten.
n = 4
r = np.arange(1, n+1)
X = stats.Normal()
Y = stats.order_statistic(X, r=r, n=n)
Y.plot()
plt.show()
Berechnen Sie die Erwartungswerte dieser Ordnungsstatistiken
Y.mean()
array([-1.02937537, -0.29701138, 0.29701138, 1.02937537])
Schlussfolgerung#
Auch wenn Veränderungen unangenehm sein können, ebnet die neue Infrastruktur den Weg zu einer verbesserten Erfahrung für Benutzer von SciPy's Wahrscheinlichkeitsverteilungen. Sie ist natürlich noch nicht vollständig! Zum Zeitpunkt der Erstellung dieses Leitfadens sind folgende Features für zukünftige Versionen geplant:
Zusätzliche eingebaute Verteilungen (neben
NormalundUniform)Diskrete Verteilungen
Kreisförmige Verteilungen, einschließlich der Möglichkeit, beliebige kontinuierliche Verteilungen um den Kreis zu wickeln
Unterstützung für andere Python Array API-kompatible Backends außer NumPy (z.B. CuPy, PyTorch, JAX)
Wie immer wird SciPy für die SciPy-Community von der SciPy-Community entwickelt. Vorschläge für weitere Features und Hilfe bei deren Implementierung werden immer gerne angenommen.
Wir hoffen, dieser Leitfaden motiviert die Vorteile des Ausprobierens der neuen Infrastruktur und vereinfacht den Prozess.