Scattered data interpolation (griddata)#
Angenommen, Sie haben mehrdimensionale Daten, zum Beispiel für eine zugrunde liegende Funktion \(f(x, y)\), von der Sie nur die Werte an Punkten (x[i], y[i]) kennen, die kein regelmäßiges Gitter bilden.
Angenommen, wir möchten die 2-D-Funktion interpolieren
>>> import numpy as np
>>> def func(x, y):
... return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2
auf einem Gitter in [0, 1]x[0, 1]
>>> grid_x, grid_y = np.meshgrid(np.linspace(0, 1, 100),
... np.linspace(0, 1, 200), indexing='ij')
aber wir kennen ihre Werte nur an 1000 Datenpunkten
>>> rng = np.random.default_rng()
>>> points = rng.random((1000, 2))
>>> values = func(points[:,0], points[:,1])
Dies kann mit griddata erfolgen – unten probieren wir alle Interpolationsmethoden aus
>>> from scipy.interpolate import griddata
>>> grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
>>> grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
>>> grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')
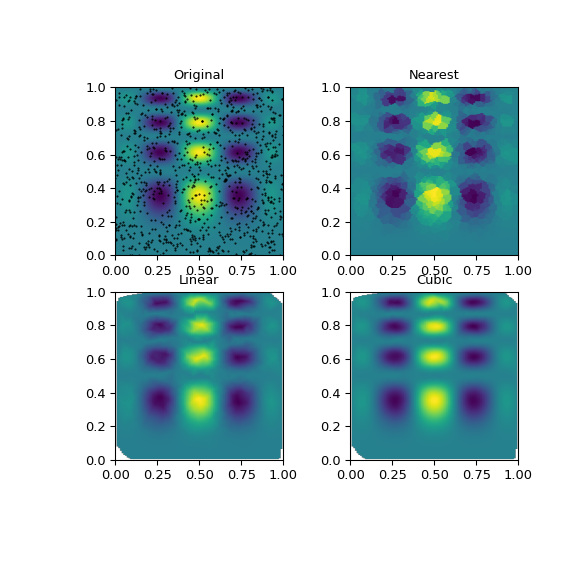
Man kann sehen, dass das exakte Ergebnis von allen Methoden bis zu einem gewissen Grad reproduziert wird, aber für diese glatte Funktion liefert der stückweise kubische Interpolant die besten Ergebnisse (schwarze Punkte zeigen die interpolierten Daten an)
>>> import matplotlib.pyplot as plt
>>> plt.subplot(221)
>>> plt.imshow(func(grid_x, grid_y).T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.plot(points[:, 0], points[:, 1], 'k.', ms=1) # data
>>> plt.title('Original')
>>> plt.subplot(222)
>>> plt.imshow(grid_z0.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Nearest')
>>> plt.subplot(223)
>>> plt.imshow(grid_z1.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Linear')
>>> plt.subplot(224)
>>> plt.imshow(grid_z2.T, extent=(0, 1, 0, 1), origin='lower')
>>> plt.title('Cubic')
>>> plt.gcf().set_size_inches(6, 6)
>>> plt.show()
Für jede Interpolationsmethode delegiert diese Funktion an ein entsprechendes Klassenobjekt – diese Klassen können auch direkt verwendet werden: NearestNDInterpolator, LinearNDInterpolator und CloughTocher2DInterpolator für stückweise kubische Interpolation in 2D.
Alle diese Interpolationsmethoden basieren auf der Triangulierung der Daten unter Verwendung der QHull-Bibliothek, die in scipy.spatial eingekapselt ist.
Hinweis
griddata basiert auf Triangulierung und ist daher für unstrukturierte, verstreute Daten geeignet. Wenn Ihre Daten auf einem vollständigen Gitter liegen, ist die griddata-Funktion – trotz ihres Namens – nicht das richtige Werkzeug. Verwenden Sie stattdessen RegularGridInterpolator.
Hinweis
Wenn die Eingabedaten so beschaffen sind, dass die Eingabedimensionen inkommensurable Einheiten aufweisen und sich um viele Größenordnungen unterscheiden, kann der Interpolant numerische Artefakte aufweisen. Erwägen Sie die Skalierung der Daten vor der Interpolation oder verwenden Sie das Schlüsselwortargument rescale=True für griddata.
Verwendung von radialen Basisfunktionen für Glättung/Interpolation#
Radiale Basisfunktionen können für die Glättung/Interpolation von verstreuten Daten in N Dimensionen verwendet werden, sollten aber mit Vorsicht bei der Extrapolation außerhalb des beobachteten Datenbereichs eingesetzt werden.
1-D-Beispiel#
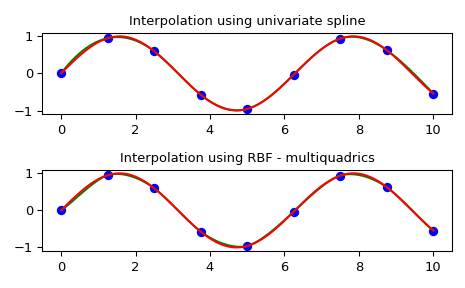
Dieses Beispiel vergleicht die Verwendung der Klassen RBFInterpolator und UnivariateSpline aus dem Modul scipy.interpolate.
>>> import numpy as np
>>> from scipy.interpolate import RBFInterpolator, InterpolatedUnivariateSpline
>>> import matplotlib.pyplot as plt
>>> # setup data
>>> x = np.linspace(0, 10, 9).reshape(-1, 1)
>>> y = np.sin(x)
>>> xi = np.linspace(0, 10, 101).reshape(-1, 1)
>>> # use fitpack2 method
>>> ius = InterpolatedUnivariateSpline(x, y)
>>> yi = ius(xi)
>>> fix, (ax1, ax2) = plt.subplots(2, 1)
>>> ax1.plot(x, y, 'bo')
>>> ax1.plot(xi, yi, 'g')
>>> ax1.plot(xi, np.sin(xi), 'r')
>>> ax1.set_title('Interpolation using univariate spline')
>>> # use RBF method
>>> rbf = RBFInterpolator(x, y)
>>> fi = rbf(xi)
>>> ax2.plot(x, y, 'bo')
>>> ax2.plot(xi, fi, 'g')
>>> ax2.plot(xi, np.sin(xi), 'r')
>>> ax2.set_title('Interpolation using RBF - multiquadrics')
>>> plt.tight_layout()
>>> plt.show()
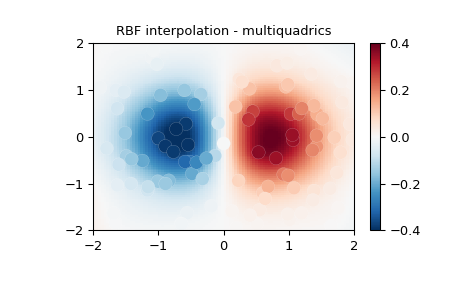
2-D-Beispiel#
Dieses Beispiel zeigt, wie verstreute 2-D-Daten interpoliert werden können
>>> import numpy as np
>>> from scipy.interpolate import RBFInterpolator
>>> import matplotlib.pyplot as plt
>>> # 2-d tests - setup scattered data
>>> rng = np.random.default_rng()
>>> xy = rng.random((100, 2))*4.0-2.0
>>> z = xy[:, 0]*np.exp(-xy[:, 0]**2-xy[:, 1]**2)
>>> edges = np.linspace(-2.0, 2.0, 101)
>>> centers = edges[:-1] + np.diff(edges[:2])[0] / 2.
>>> x_i, y_i = np.meshgrid(centers, centers)
>>> x_i = x_i.reshape(-1, 1)
>>> y_i = y_i.reshape(-1, 1)
>>> xy_i = np.concatenate([x_i, y_i], axis=1)
>>> # use RBF
>>> rbf = RBFInterpolator(xy, z, epsilon=2)
>>> z_i = rbf(xy_i)
>>> # plot the result
>>> fig, ax = plt.subplots()
>>> X_edges, Y_edges = np.meshgrid(edges, edges)
>>> lims = dict(cmap='RdBu_r', vmin=-0.4, vmax=0.4)
>>> mapping = ax.pcolormesh(
... X_edges, Y_edges, z_i.reshape(100, 100),
... shading='flat', **lims
... )
>>> ax.scatter(xy[:, 0], xy[:, 1], 100, z, edgecolor='w', lw=0.1, **lims)
>>> ax.set(
... title='RBF interpolation - multiquadrics',
... xlim=(-2, 2),
... ylim=(-2, 2),
... )
>>> fig.colorbar(mapping)