Tipps und Tricks zur Extrapolation#
Die Handhabung von Extrapolation – die Auswertung von Interpolatoren an Abfragepunkten außerhalb des Definitionsbereichs der interpolierten Daten – ist nicht bei allen Routinen in scipy.interpolate vollständig konsistent. Verschiedene Interpolatoren verwenden unterschiedliche Sätze von Schlüsselwortargumenten, um das Verhalten außerhalb des Datenbereichs zu steuern: einige verwenden extrapolate=True/False/None, einige erlauben das Schlüsselwort fill_value. Details für jede spezifische Interpolationsroutine finden Sie in der API-Dokumentation.
Abhängig vom jeweiligen Problem sind die verfügbaren Schlüsselwörter möglicherweise nicht ausreichend. Besonderes Augenmerk muss der Extrapolation von nicht-linearen Interpolatoren gewidmet werden. Sehr oft machen die extrapolierten Ergebnisse bei zunehmender Entfernung vom Datenbereich weniger Sinn. Dies ist natürlich zu erwarten: Ein Interpolator kennt nur die Daten innerhalb des Datenbereichs.
Wenn die standardmäßigen extrapolierten Ergebnisse nicht ausreichend sind, müssen die Benutzer den gewünschten Extrapolationsmodus selbst implementieren.
In diesem Tutorial betrachten wir mehrere ausgearbeitete Beispiele, in denen wir sowohl die Verwendung der verfügbaren Schlüsselwörter als auch die manuelle Implementierung gewünschter Extrapolationsmodi demonstrieren. Diese Beispiele sind möglicherweise nicht für Ihr spezifisches Problem relevant; sie sind nicht unbedingt Best Practices; und sie sind bewusst auf das Nötigste reduziert, um die Hauptideen zu demonstrieren, in der Hoffnung, dass sie als Inspiration für die Handhabung Ihres spezifischen Problems dienen.
interp1d : Replikation der linken und rechten Füllwerte von numpy.interp#
TL;DR: Verwenden Sie fill_value=(links, rechts)
numpy.interp verwendet konstante Extrapolation und erweitert standardmäßig die ersten und letzten Werte des y-Arrays im Interpolationsintervall: die Ausgabe von np.interp(xnew, x, y) ist y[0] für xnew < x[0] und y[-1] für xnew > x[-1].
Standardmäßig weigert sich interp1d zu extrapolieren und löst eine ValueError aus, wenn sie an einem Datenpunkt außerhalb des Interpolationsbereichs ausgewertet wird. Dies kann durch das Argument bounds_error=False ausgeschaltet werden: Dann setzt interp1d die Werte außerhalb des Bereichs mit fill_value, das standardmäßig nan ist.
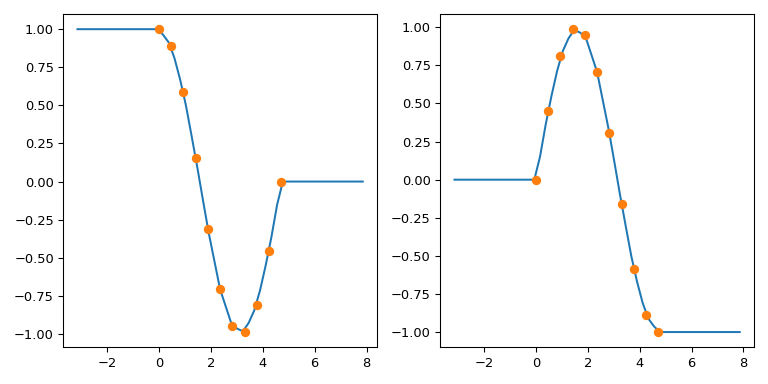
Um das Verhalten von numpy.interp mit interp1d zu simulieren, können Sie die Tatsache nutzen, dass es ein 2-Tupel als fill_value unterstützt. Die Tupel-Elemente werden dann für xnew < min(x) und x > max(x) gefüllt. Für mehrdimensionale y müssen diese Elemente die gleiche Form wie y haben oder dorthin broadcastbar sein.
Zur Veranschaulichung
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
x = np.linspace(0, 1.5*np.pi, 11)
y = np.column_stack((np.cos(x), np.sin(x))) # y.shape is (11, 2)
func = interp1d(x, y,
axis=0, # interpolate along columns
bounds_error=False,
kind='linear',
fill_value=(y[0], y[-1]))
xnew = np.linspace(-np.pi, 2.5*np.pi, 51)
ynew = func(xnew)
fix, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 4))
ax1.plot(xnew, ynew[:, 0])
ax1.plot(x, y[:, 0], 'o')
ax2.plot(xnew, ynew[:, 1])
ax2.plot(x, y[:, 1], 'o')
plt.tight_layout()
CubicSpline erweitert die Randbedingungen#
CubicSpline benötigt zwei zusätzliche Randbedingungen, die durch den Parameter bc_type gesteuert werden. Dieser Parameter kann entweder explizite Werte von Ableitungen an den Rändern auflisten oder hilfreiche Aliase verwenden. Zum Beispiel setzt bc_type="clamped" die ersten Ableitungen auf Null, bc_type="natural" setzt die zweiten Ableitungen auf Null (zwei weitere erkannte Zeichenfolgen sind „periodic“ und „not-a-knot“).
Während die Extrapolation durch die Randbedingung gesteuert wird, ist der Zusammenhang nicht sehr intuitiv. Man könnte zum Beispiel erwarten, dass bei bc_type="natural" die Extrapolation linear ist. Diese Erwartung ist zu stark: Jede Randbedingung setzt die Ableitungen an einem einzigen Punkt, und zwar *am Rand*. Die Extrapolation erfolgt von den ersten und letzten Polynomstücken, die – bei einem natürlichen Spline – kubisch mit einer zweiten Ableitung von Null an einem gegebenen Punkt sind.
Ein anderer Weg, warum diese Erwartung zu stark ist, ist die Betrachtung eines Datensatzes mit nur drei Datenpunkten, bei dem der Spline zwei Polynomstücke hat. Um linear zu extrapolieren, impliziert diese Erwartung, dass beide Stücke linear sind. Aber dann können zwei lineare Stücke nicht an einem mittleren Punkt mit einer kontinuierlichen zweiten Ableitung übereinstimmen! (Es sei denn, natürlich, alle drei Datenpunkte liegen tatsächlich auf einer einzigen geraden Linie).
Zur Veranschaulichung des Verhaltens betrachten wir einen synthetischen Datensatz und vergleichen mehrere Randbedingungen.
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
xs = [1, 2, 3, 4, 5, 6, 7, 8]
ys = [4.5, 3.6, 1.6, 0.0, -3.3, -3.1, -1.8, -1.7]
notaknot = CubicSpline(xs, ys, bc_type='not-a-knot')
natural = CubicSpline(xs, ys, bc_type='natural')
clamped = CubicSpline(xs, ys, bc_type='clamped')
xnew = np.linspace(min(xs) - 4, max(xs) + 4, 101)
splines = [notaknot, natural, clamped]
titles = ['not-a-knot', 'natural', 'clamped']
fig, axs = plt.subplots(3, 3, figsize=(12, 12))
for i in [0, 1, 2]:
for j, spline, title in zip(range(3), splines, titles):
axs[i, j].plot(xs, spline(xs, nu=i),'o')
axs[i, j].plot(xnew, spline(xnew, nu=i),'-')
axs[i, j].set_title(f'{title}, deriv={i}')
plt.tight_layout()
plt.show()

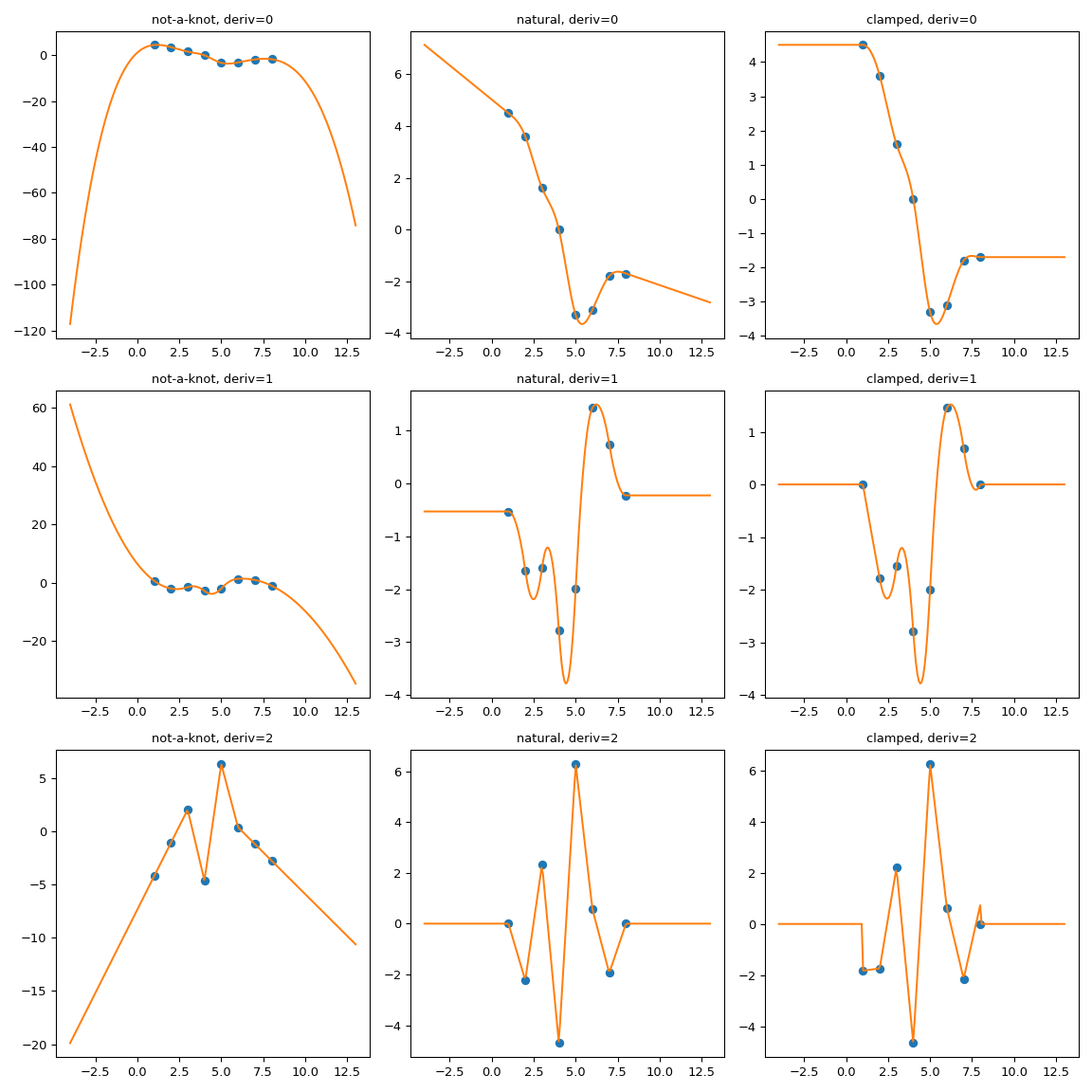
Es ist deutlich zu sehen, dass der natürliche Spline an den Rändern die Null-Zweit-Ableitung hat, aber die Extrapolation ist nicht-linear. bc_type="clamped" zeigt ein ähnliches Verhalten: Die ersten Ableitungen sind nur genau am Rand gleich Null. In allen Fällen erfolgt die Extrapolation durch Erweiterung der ersten und letzten Polynomstücke des Splines, was auch immer diese sein mögen.
Eine mögliche Methode, die Extrapolation zu erzwingen, ist die Erweiterung des Interpolationsbereichs um erste und letzte Polynomstücke mit den gewünschten Eigenschaften.
Hier verwenden wir die Methode extend der CubicSpline-Superklasse, PPoly, um zwei zusätzliche Haltepunkte hinzuzufügen und sicherzustellen, dass die zusätzlichen Polynomstücke die Werte der Ableitungen beibehalten. Dann erfolgt die Extrapolation mithilfe dieser beiden zusätzlichen Intervalle.
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CubicSpline
def add_boundary_knots(spline):
"""
Add knots infinitesimally to the left and right.
Additional intervals are added to have zero 2nd and 3rd derivatives,
and to maintain the first derivative from whatever boundary condition
was selected. The spline is modified in place.
"""
# determine the slope at the left edge
leftx = spline.x[0]
lefty = spline(leftx)
leftslope = spline(leftx, nu=1)
# add a new breakpoint just to the left and use the
# known slope to construct the PPoly coefficients.
leftxnext = np.nextafter(leftx, leftx - 1)
leftynext = lefty + leftslope*(leftxnext - leftx)
leftcoeffs = np.array([0, 0, leftslope, leftynext])
spline.extend(leftcoeffs[..., None], np.r_[leftxnext])
# repeat with additional knots to the right
rightx = spline.x[-1]
righty = spline(rightx)
rightslope = spline(rightx,nu=1)
rightxnext = np.nextafter(rightx, rightx + 1)
rightynext = righty + rightslope * (rightxnext - rightx)
rightcoeffs = np.array([0, 0, rightslope, rightynext])
spline.extend(rightcoeffs[..., None], np.r_[rightxnext])
xs = [1, 2, 3, 4, 5, 6, 7, 8]
ys = [4.5, 3.6, 1.6, 0.0, -3.3, -3.1, -1.8, -1.7]
notaknot = CubicSpline(xs,ys, bc_type='not-a-knot')
# not-a-knot does not require additional intervals
natural = CubicSpline(xs,ys, bc_type='natural')
# extend the natural natural spline with linear extrapolating knots
add_boundary_knots(natural)
clamped = CubicSpline(xs,ys, bc_type='clamped')
# extend the clamped spline with constant extrapolating knots
add_boundary_knots(clamped)
xnew = np.linspace(min(xs) - 5, max(xs) + 5, 201)
fig, axs = plt.subplots(3, 3,figsize=(12,12))
splines = [notaknot, natural, clamped]
titles = ['not-a-knot', 'natural', 'clamped']
for i in [0, 1, 2]:
for j, spline, title in zip(range(3), splines, titles):
axs[i, j].plot(xs, spline(xs, nu=i),'o')
axs[i, j].plot(xnew, spline(xnew, nu=i),'-')
axs[i, j].set_title(f'{title}, deriv={i}')
plt.tight_layout()
plt.show()
Manuelle Implementierung der Asymptotik#
Der vorherige Trick, den Interpolationsbereich zu erweitern, beruht auf der Methode CubicSpline.extend. Eine etwas allgemeinere Alternative ist die Implementierung einer Wrapper-Funktion, die das Verhalten außerhalb des Bereichs explizit behandelt. Betrachten wir ein ausgearbeitetes Beispiel.
Das Setup#
Nehmen wir an, wir wollen für einen gegebenen Wert von \(a\) die Gleichung lösen
(Eine Anwendung, bei der solche Gleichungen auftreten, ist die Lösung von Energieniveaus eines Quantenteilchens). Der Einfachheit halber betrachten wir nur \(x\in (0, \pi/2)\).
Das einmalige Lösen dieser Gleichung ist unkompliziert.
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import brentq
def f(x, a):
return a*x - 1/np.tan(x)
a = 3
x0 = brentq(f, 1e-16, np.pi/2, args=(a,)) # here we shift the left edge
# by a machine epsilon to avoid
# a division by zero at x=0
xx = np.linspace(0.2, np.pi/2, 101)
plt.plot(xx, a*xx, '--')
plt.plot(xx, 1/np.tan(xx), '--')
plt.plot(x0, a*x0, 'o', ms=12)
plt.text(0.1, 0.9, fr'$x_0 = {x0:.3f}$',
transform=plt.gca().transAxes, fontsize=16)
plt.show()

Wenn wir sie jedoch mehrmals lösen müssen (z. B. um aufgrund der Periodizität der tan-Funktion *eine Reihe* von Wurzeln zu finden), werden wiederholte Aufrufe von scipy.optimize.brentq prohibitiv teuer.
Um dieses Problem zu umgehen, tabellieren wir \(y = ax - 1/\tan{x}\) und interpolieren sie auf dem tabellierten Gitter. Tatsächlich werden wir die *inverse* Interpolation verwenden: Wir interpolieren die Werte von \(x\) gegen \(у\). Auf diese Weise wird das Lösen der ursprünglichen Gleichung einfach zu einer Auswertung der interpolierten Funktion an Null als \(y\)-Argument.
Um die Interpolationsgenauigkeit zu verbessern, werden wir das Wissen über die Ableitungen der tabellierten Funktion nutzen. Wir werden BPoly.from_derivatives verwenden, um einen kubischen Interpolanten zu konstruieren (alternativ hätten wir auch CubicHermiteSpline verwenden können).
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import BPoly
def f(x, a):
return a*x - 1/np.tan(x)
xleft, xright = 0.2, np.pi/2
x = np.linspace(xleft, xright, 11)
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
for j, a in enumerate([3, 93]):
y = f(x, a)
dydx = a + 1./np.sin(x)**2 # d(ax - 1/tan(x)) / dx
dxdy = 1 / dydx # dx/dy = 1 / (dy/dx)
xdx = np.c_[x, dxdy]
spl = BPoly.from_derivatives(y, xdx) # inverse interpolation
yy = np.linspace(f(xleft, a), f(xright, a), 51)
ax[j].plot(yy, spl(yy), '--')
ax[j].plot(y, x, 'o')
ax[j].set_xlabel(r'$y$')
ax[j].set_ylabel(r'$x$')
ax[j].set_title(rf'$a = {a}$')
ax[j].plot(0, spl(0), 'o', ms=12)
ax[j].text(0.1, 0.85, fr'$x_0 = {spl(0):.3f}$',
transform=ax[j].transAxes, fontsize=18)
ax[j].grid(True)
plt.tight_layout()
plt.show()
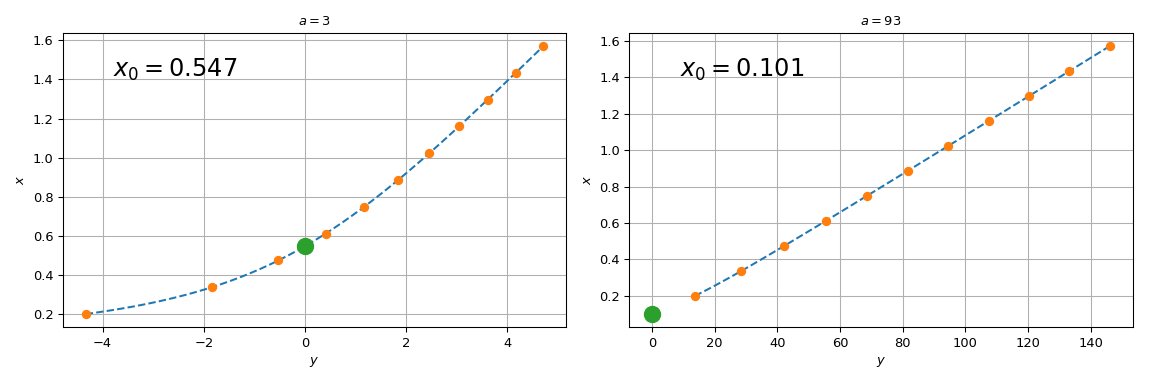
Beachten Sie, dass für \(a=3\) spl(0) mit dem obigen brentq-Aufruf übereinstimmt, während für \(a = 93\) der Unterschied beträchtlich ist. Der Grund, warum das Verfahren bei großen \(a\) zu versagen beginnt, ist, dass die gerade Linie \(y = ax\) sich der vertikalen Achse nähert und die Wurzel der ursprünglichen Gleichung sich \(x=0\) nähert. Da wir die ursprüngliche Funktion auf einem endlichen Gitter tabelliert haben, beinhaltet spl(0) eine Extrapolation für zu große Werte von \(a\). Sich auf Extrapolation zu verlassen, birgt die Gefahr von Genauigkeitsverlust und sollte am besten vermieden werden.
Nutzen Sie die bekannte Asymptotik#
Betrachten wir die ursprüngliche Gleichung, stellen wir fest, dass für \(x\to 0\) gilt \(\tan(x) = x + O(x^3)\), und die ursprüngliche Gleichung wird zu
so dass \(x_0 \approx 1/\sqrt{a}\) für \(a \gg 1\) gilt.
Wir werden dies verwenden, um eine Klasse zu erstellen, die zwischen Interpolation und der Verwendung dieses bekannten asymptotischen Verhaltens für Daten außerhalb des Bereichs wechselt. Eine grundlegende Implementierung könnte wie folgt aussehen:
class RootWithAsymptotics:
def __init__(self, a):
# construct the interpolant
xleft, xright = 0.2, np.pi/2
x = np.linspace(xleft, xright, 11)
y = f(x, a)
dydx = a + 1./np.sin(x)**2 # d(ax - 1/tan(x)) / dx
dxdy = 1 / dydx # dx/dy = 1 / (dy/dx)
# inverse interpolation
self.spl = BPoly.from_derivatives(y, np.c_[x, dxdy])
self.a = a
def root(self):
out = self.spl(0)
asympt = 1./np.sqrt(self.a)
return np.where(spl.x.min() < asympt, out, asympt)
Und dann
>>> r = RootWithAsymptotics(93)
>>> r.root()
array(0.10369517)
was sich vom extrapolierten Ergebnis unterscheidet und mit dem brentq-Aufruf übereinstimmt.
Beachten Sie, dass diese Implementierung absichtlich vereinfacht ist. Aus API-Sicht möchten Sie vielleicht stattdessen die Methode __call__ implementieren, damit die volle Abhängigkeit von x von y verfügbar ist. Aus numerischer Sicht ist mehr Arbeit erforderlich, um sicherzustellen, dass der Wechsel zwischen Interpolation und Asymptotik tief genug in das asymptotische Regime erfolgt, so dass die resultierende Funktion an der Wechselstelle glatt genug ist.
In diesem Beispiel haben wir auch künstlich das Problem auf nur ein Periodizitätsintervall der tan-Funktion beschränkt und nur \(a > 0\) behandelt. Für negative Werte von \(a\) müssten wir die andere Asymptotik für \(x\to \pi\) implementieren.
Die Grundidee ist jedoch dieselbe.
Extrapolation in D > 1#
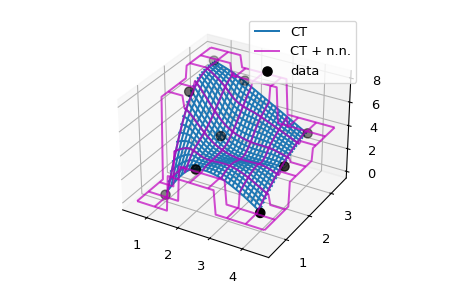
Die Grundidee der manuellen Implementierung von Extrapolation in einer Wrapper-Klasse oder Funktion lässt sich leicht auf höhere Dimensionen verallgemeinern. Als Beispiel betrachten wir ein C1-glattes Interpolationsproblem von 2D-Daten unter Verwendung von CloughTocher2DInterpolator. Standardmäßig füllt er Werte außerhalb des Bereichs mit nans, und wir möchten stattdessen für jeden Abfragepunkt den Wert seines nächsten Nachbarn verwenden.
Da CloughTocher2DInterpolator entweder 2D-Daten oder eine Delaunay-Triangulierung der Datenpunkte akzeptiert, wäre der effiziente Weg, die nächsten Nachbarn von Abfragepunkten zu finden, die Triangulierung zu konstruieren (mit scipy.spatial-Tools) und sie zu verwenden, um die nächsten Nachbarn auf der konvexen Hülle der Daten zu finden.
Wir werden stattdessen eine einfachere, naive Methode verwenden und uns auf das Schleifen über den gesamten Datensatz mittels NumPy-Broadcasting verlassen.
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import CloughTocher2DInterpolator as CT
def my_CT(xy, z):
"""CT interpolator + nearest-neighbor extrapolation.
Parameters
----------
xy : ndarray, shape (npoints, ndim)
Coordinates of data points
z : ndarray, shape (npoints)
Values at data points
Returns
-------
func : callable
A callable object which mirrors the CT behavior,
with an additional neareast-neighbor extrapolation
outside of the data range.
"""
x = xy[:, 0]
y = xy[:, 1]
f = CT(xy, z)
# this inner function will be returned to a user
def new_f(xx, yy):
# evaluate the CT interpolator. Out-of-bounds values are nan.
zz = f(xx, yy)
nans = np.isnan(zz)
if nans.any():
# for each nan point, find its nearest neighbor
inds = np.argmin(
(x[:, None] - xx[nans])**2 +
(y[:, None] - yy[nans])**2
, axis=0)
# ... and use its value
zz[nans] = z[inds]
return zz
return new_f
# Now illustrate the difference between the original ``CT`` interpolant
# and ``my_CT`` on a small example:
x = np.array([1, 1, 1, 2, 2, 2, 4, 4, 4])
y = np.array([1, 2, 3, 1, 2, 3, 1, 2, 3])
z = np.array([0, 7, 8, 3, 4, 7, 1, 3, 4])
xy = np.c_[x, y]
lut = CT(xy, z)
lut2 = my_CT(xy, z)
X = np.linspace(min(x) - 0.5, max(x) + 0.5, 71)
Y = np.linspace(min(y) - 0.5, max(y) + 0.5, 71)
X, Y = np.meshgrid(X, Y)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_wireframe(X, Y, lut(X, Y), label='CT')
ax.plot_wireframe(X, Y, lut2(X, Y), color='m',
cstride=10, rstride=10, alpha=0.7, label='CT + n.n.')
ax.scatter(x, y, z, 'o', color='k', s=48, label='data')
ax.legend()
plt.tight_layout()