Wahrscheinlichkeitsverteilungen#
SciPy verfügt über zwei Infrastrukturen für die Arbeit mit Wahrscheinlichkeitsverteilungen. Dieses Tutorial ist für die ältere gedacht, die viele vordefinierte Verteilungen hat; die neue Infrastruktur kann jedoch mit den meisten davon verwendet werden und bietet viele Vorteile. Informationen zur neuen Infrastruktur finden Sie in Anleitung zur Zufallsvariablen-Infrastruktur.
Es wurden zwei allgemeine Verteilungsklassen implementiert, um kontinuierliche Zufallsvariablen und diskrete Zufallsvariablen zu kapseln. Über 100 kontinuierliche Zufallsvariablen (RVs) und 20 diskrete Zufallsvariablen wurden mit diesen Klassen implementiert. Informationen zu einzelnen Verteilungen finden Sie unter Kontinuierliche statistische Verteilungen und Diskrete statistische Verteilungen.
Alle Statistikfunktionen befinden sich im Unterpaket scipy.stats. Eine ziemlich vollständige Liste dieser Funktionen und verfügbaren Zufallsvariablen kann auch aus dem Docstring des Stats-Unterpakets abgerufen werden.
In der folgenden Diskussion konzentrieren wir uns hauptsächlich auf kontinuierliche Zufallsvariablen. Fast alles gilt auch für diskrete Variablen, aber wir weisen hier auf einige Unterschiede hin: Spezifische Punkte für diskrete Verteilungen.
In den folgenden Codebeispielen gehen wir davon aus, dass das Paket scipy.stats importiert wird als
>>> from scipy import stats
und in einigen Fällen gehen wir davon aus, dass einzelne Objekte importiert werden als
>>> from scipy.stats import norm
Alle Verteilungen
Hilfe erhalten#
Zuallererst sind alle Verteilungen mit Hilfsfunktionen ausgestattet. Um nur einige grundlegende Informationen zu erhalten, drucken wir den entsprechenden Docstring: print(stats.norm.__doc__).
Um den Wertebereich, d.h. die oberen und unteren Grenzen der Verteilung, zu finden, rufen Sie auf
>>> print('bounds of distribution lower: %s, upper: %s' % norm.support())
bounds of distribution lower: -inf, upper: inf
Wir können alle Methoden und Eigenschaften der Verteilung mit dir(norm) auflisten. Wie sich herausstellt, sind einige der Methoden privat, obwohl sie nicht so benannt sind (ihre Namen beginnen nicht mit einem führenden Unterstrich), z.B. veccdf, nur für interne Berechnungen verfügbar (diese Methoden geben Warnungen aus, wenn man versucht, sie zu verwenden, und werden irgendwann entfernt).
Um die *echten* Hauptmethoden zu erhalten, listen wir die Methoden der "eingefrorenen" Verteilung auf. (Wir erklären die Bedeutung einer *eingefrorenen* Verteilung weiter unten).
>>> rv = norm()
>>> dir(rv) # reformatted
['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__',
'__format__', '__ge__', '__getattribute__', '__gt__', '__hash__',
'__init__', '__le__', '__lt__', '__module__', '__ne__', '__new__',
'__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__',
'__str__', '__subclasshook__', '__weakref__', 'a', 'args', 'b', 'cdf',
'dist', 'entropy', 'expect', 'interval', 'isf', 'kwds', 'logcdf',
'logpdf', 'logpmf', 'logsf', 'mean', 'median', 'moment', 'pdf', 'pmf',
'ppf', 'random_state', 'rvs', 'sf', 'stats', 'std', 'var']
Schließlich können wir die Liste der verfügbaren Verteilungen durch Introspektion erhalten
>>> dist_continu = [d for d in dir(stats) if
... isinstance(getattr(stats, d), stats.rv_continuous)]
>>> dist_discrete = [d for d in dir(stats) if
... isinstance(getattr(stats, d), stats.rv_discrete)]
>>> print('number of continuous distributions: %d' % len(dist_continu))
number of continuous distributions: 109
>>> print('number of discrete distributions: %d' % len(dist_discrete))
number of discrete distributions: 21
Gemeinsame Methoden#
Die wichtigsten öffentlichen Methoden für kontinuierliche Zufallsvariablen sind
rvs: Zufallsvariaten
pdf: Wahrscheinlichkeitsdichtefunktion
cdf: Kumulative Verteilungsfunktion
sf: Überlebensfunktion (1-CDF)
ppf: Perzentilpunktfunktion (Umkehrfunktion der CDF)
isf: Inverse Überlebensfunktion (Umkehrfunktion der SF)
stats: Mittelwert, Varianz, (Fisher'sche) Schiefe oder (Fisher'sche) Kurtosis zurückgeben
moment: nicht-zentrale Momente der Verteilung
Nehmen wir als Beispiel eine Normalverteilung.
>>> norm.cdf(0)
0.5
Um die cdf an einer Reihe von Punkten zu berechnen, können wir eine Liste oder ein Numpy-Array übergeben.
>>> norm.cdf([-1., 0, 1])
array([ 0.15865525, 0.5, 0.84134475])
>>> import numpy as np
>>> norm.cdf(np.array([-1., 0, 1]))
array([ 0.15865525, 0.5, 0.84134475])
Somit sind die grundlegenden Methoden, wie pdf, cdf usw. vektorisiert.
Andere allgemein nützliche Methoden werden ebenfalls unterstützt
>>> norm.mean(), norm.std(), norm.var()
(0.0, 1.0, 1.0)
>>> norm.stats(moments="mv")
(array(0.0), array(1.0))
Um den Median einer Verteilung zu finden, können wir die Perzentilpunktfunktion ppf verwenden, die die Umkehrfunktion der cdf ist
>>> norm.ppf(0.5)
0.0
Um eine Folge von Zufallsvariaten zu erzeugen, verwenden Sie das Schlüsselwortargument size
>>> norm.rvs(size=3)
array([-0.35687759, 1.34347647, -0.11710531]) # random
Denken Sie nicht, dass norm.rvs(5) 5 Variaten erzeugt
>>> norm.rvs(5)
5.471435163732493 # random
Hier wird die 5 ohne Schlüsselwort als erstes mögliches Schlüsselwortargument, loc, interpretiert, was das erste von zwei Schlüsselwortargumenten ist, die von allen kontinuierlichen Verteilungen angenommen werden. Dies bringt uns zum Thema des nächsten Unterabschnitts.
Zufallszahlengenerierung#
Das Ziehen von Zufallszahlen basiert auf Generatoren aus dem Paket numpy.random. In den obigen Beispielen ist der spezifische Strom von Zufallszahlen nicht über Ausführungen hinweg reproduzierbar. Um Reproduzierbarkeit zu erreichen, können Sie einen Zufallszahlengenerator explizit *seed*en. In NumPy ist ein Generator eine Instanz von numpy.random.Generator. Hier ist der kanonische Weg, einen Generator zu erstellen
>>> from numpy.random import default_rng
>>> rng = default_rng()
Und das Festlegen des Seeds kann wie folgt erfolgen
>>> # do NOT copy this value
>>> rng = default_rng(301439351238479871608357552876690613766)
Warnung
Verwenden Sie diese Zahl oder gängige Werte wie 0 nicht. Die Verwendung einer kleinen Menge von Seeds zur Instanziierung großer Zustandsräume bedeutet, dass es einige Anfangszustände gibt, die unmöglich zu erreichen sind. Dies führt zu Verzerrungen, wenn jeder solche Werte verwendet. Eine gute Möglichkeit, einen Seed zu erhalten, ist die Verwendung einer numpy.random.SeedSequence
>>> from numpy.random import SeedSequence
>>> print(SeedSequence().entropy)
301439351238479871608357552876690613766 # random
Der Parameter random_state in den Verteilungen akzeptiert eine Instanz der Klasse numpy.random.Generator oder eine Ganzzahl, die dann verwendet wird, um ein internes Generator -Objekt zu seeden
>>> norm.rvs(size=5, random_state=rng)
array([ 0.47143516, -1.19097569, 1.43270697, -0.3126519 , -0.72058873]) # random
Weitere Informationen finden Sie in der Dokumentation von NumPy.
Um mehr über die in SciPy implementierten Zufallszahlensampler zu erfahren, siehe Tutorial zur nicht-gleichmäßigen Zufallszahlenerzeugung und Quasi-Monte-Carlo-Tutorial
Verschiebung und Skalierung#
Alle kontinuierlichen Verteilungen verwenden die Schlüsselwortparameter loc und scale, um die Lage und Skalierung der Verteilung anzupassen. Für die Standardnormalverteilung ist die Lage der Mittelwert und die Skalierung die Standardabweichung.
>>> norm.stats(loc=3, scale=4, moments="mv")
(array(3.0), array(16.0))
In vielen Fällen wird die standardisierte Verteilung für eine Zufallsvariable X durch die Transformation (X - loc) / scale erhalten. Die Standardwerte sind loc = 0 und scale = 1.
Die clevere Nutzung von loc und scale kann helfen, die Standardverteilungen auf vielfältige Weise zu modifizieren. Um die Skalierung weiter zu veranschaulichen, ist die cdf einer exponentiell verteilten Zufallsvariablen mit dem Mittelwert \(1/\lambda\) gegeben durch
Durch Anwenden der obigen Skalierungsregel kann man sehen, dass durch die Wahl von scale = 1./lambda die richtige Skalierung erzielt wird.
>>> from scipy.stats import expon
>>> expon.mean(scale=3.)
3.0
Hinweis
Verteilungen, die Formparameter verwenden, erfordern möglicherweise mehr als eine einfache Anwendung von loc und/oder scale, um die gewünschte Form zu erreichen. Zum Beispiel ist die Verteilung von Längen 2D-Vektoren, die durch eine konstante Vektorlänge \(R\) und unabhängige N(0, \(\sigma^2\)) Abweichungen in jeder Komponente gestört werden, rice(\(R/\sigma\), scale= \(\sigma\)). Das erste Argument ist ein Formparameter, der zusammen mit \(x\) skaliert werden muss.
Die Gleichverteilung ist ebenfalls interessant
>>> from scipy.stats import uniform
>>> uniform.cdf([0, 1, 2, 3, 4, 5], loc=1, scale=4)
array([ 0. , 0. , 0.25, 0.5 , 0.75, 1. ])
Erinnern wir uns schließlich aus dem vorherigen Absatz daran, dass uns das Problem mit der Bedeutung von norm.rvs(5) verbleibt. Wenn eine Verteilung so aufgerufen wird, wird das erste Argument, also die 5, zum Setzen des loc Parameters verwendet. Sehen wir uns das an
>>> np.mean(norm.rvs(5, size=500))
5.0098355106969992 # random
Somit erklärt sich die Ausgabe des Beispiels des letzten Abschnitts: norm.rvs(5) erzeugt eine einzelne normalverteilte Zufallsvariante mit dem Mittelwert loc=5, aufgrund der Standardeinstellung size=1.
Wir empfehlen, die Parameter loc und scale explizit festzulegen, indem die Werte als Schlüsselwörter und nicht als Argumente übergeben werden. Wiederholungen können bei der Verwendung mehrerer Methoden für eine bestimmte RV minimiert werden, indem die Technik des Einfrierens einer Verteilung verwendet wird, wie unten erläutert.
Formparameter#
Während eine allgemeine kontinuierliche Zufallsvariable mit den Parametern loc und scale verschoben und skaliert werden kann, erfordern einige Verteilungen zusätzliche Formparameter. Zum Beispiel die Gamma-Verteilung mit der Dichte
benötigt den Formparameter \(a\). Beachten Sie, dass die Einstellung von \(\lambda\) durch Setzen des Schlüsselworts scale auf \(1/\lambda\) erreicht werden kann.
Lassen Sie uns die Anzahl und den Namen der Formparameter der Gamma-Verteilung überprüfen. (Wir wissen aus dem Obigen, dass dies 1 sein sollte.)
>>> from scipy.stats import gamma
>>> gamma.numargs
1
>>> gamma.shapes
'a'
Nun setzen wir den Wert der Formvariable auf 1, um die Exponentialverteilung zu erhalten, damit wir leicht vergleichen können, ob wir die erwarteten Ergebnisse erhalten.
>>> gamma(1, scale=2.).stats(moments="mv")
(array(2.0), array(4.0))
Beachten Sie, dass wir Formparameter auch als Schlüsselwörter angeben können
>>> gamma(a=1, scale=2.).stats(moments="mv")
(array(2.0), array(4.0))
Einfrieren einer Verteilung#
Das wiederholte Übergeben der Schlüsselwörter loc und scale kann recht lästig sein. Das Konzept des *Einfrierens* einer RV wird verwendet, um solche Probleme zu lösen.
>>> rv = gamma(1, scale=2.)
Durch die Verwendung von rv müssen wir die Skalierungs- oder Formparameter nicht mehr angeben. Somit können Verteilungen auf zwei Arten verwendet werden: entweder durch Übergabe aller Verteilungsparameter an jeden Methodenaufruf (wie wir es zuvor getan haben) oder durch Einfrieren der Parameter für die Instanz der Verteilung. Lassen Sie uns das überprüfen
>>> rv.mean(), rv.std()
(2.0, 2.0)
Dies ist tatsächlich das, was wir erhalten sollten.
Broadcasting#
Die grundlegenden Methoden pdf usw. erfüllen die üblichen Numpy-Broadcasting-Regeln. Wir können zum Beispiel die kritischen Werte für den oberen Schwanz der t-Verteilung für verschiedene Wahrscheinlichkeiten und Freiheitsgrade berechnen.
>>> stats.t.isf([0.1, 0.05, 0.01], [[10], [11]])
array([[ 1.37218364, 1.81246112, 2.76376946],
[ 1.36343032, 1.79588482, 2.71807918]])
Hier enthält die erste Zeile die kritischen Werte für 10 Freiheitsgrade und die zweite Zeile für 11 Freiheitsgrade (d.o.f.). Somit ergibt die Anwendung der Broadcasting-Regeln dasselbe Ergebnis wie zweimaliger Aufruf von isf
>>> stats.t.isf([0.1, 0.05, 0.01], 10)
array([ 1.37218364, 1.81246112, 2.76376946])
>>> stats.t.isf([0.1, 0.05, 0.01], 11)
array([ 1.36343032, 1.79588482, 2.71807918])
Wenn das Array mit Wahrscheinlichkeiten, d.h. [0.1, 0.05, 0.01] und das Array der Freiheitsgrade, d.h. [10, 11, 12], die gleiche Array-Form haben, wird eine elementweise Übereinstimmung verwendet. Als Beispiel können wir den 10%-Schwanz für 10 d.o.f., den 5%-Schwanz für 11 d.o.f. und den 1%-Schwanz für 12 d.o.f. erhalten, indem wir aufrufen
>>> stats.t.isf([0.1, 0.05, 0.01], [10, 11, 12])
array([ 1.37218364, 1.79588482, 2.68099799])
Spezifische Punkte für diskrete Verteilungen#
Diskrete Verteilungen haben größtenteils dieselben grundlegenden Methoden wie kontinuierliche Verteilungen. Die Funktion pdf wird jedoch durch die Wahrscheinlichkeitsmassenfunktion pmf ersetzt, es sind keine Schätzmethoden wie fit verfügbar, und scale ist kein gültiger Schlüsselwortparameter. Der Lageparameter, das Schlüsselwort loc, kann weiterhin zur Verschiebung der Verteilung verwendet werden.
Die Berechnung der cdf erfordert einige zusätzliche Aufmerksamkeit. Im Fall einer kontinuierlichen Verteilung ist die kumulative Verteilungsfunktion in den meisten Standardfällen streng monoton steigend in den Grenzen (a,b) und hat daher eine eindeutige Umkehrfunktion. Die cdf einer diskreten Verteilung ist jedoch eine Stufenfunktion, daher erfordert die Umkehrfunktion der cdf, d.h. die Perzentilpunktfunktion, eine andere Definition
ppf(q) = min{x : cdf(x) >= q, x integer}
Weitere Informationen finden Sie in der Dokumentation hier.
Wir können die hypergeometrische Verteilung als Beispiel betrachten
>>> from scipy.stats import hypergeom
>>> [M, n, N] = [20, 7, 12]
Wenn wir die cdf an einigen ganzzahligen Punkten verwenden und dann die ppf an diesen cdf-Werten auswerten, erhalten wir die ursprünglichen Ganzzahlen zurück, zum Beispiel
>>> x = np.arange(4) * 2
>>> x
array([0, 2, 4, 6])
>>> prb = hypergeom.cdf(x, M, n, N)
>>> prb
array([ 1.03199174e-04, 5.21155831e-02, 6.08359133e-01,
9.89783282e-01])
>>> hypergeom.ppf(prb, M, n, N)
array([ 0., 2., 4., 6.])
Wenn wir Werte verwenden, die nicht an den Knicken der cdf-Stufenfunktion liegen, erhalten wir die nächsthöhere Ganzzahl zurück
>>> hypergeom.ppf(prb + 1e-8, M, n, N)
array([ 1., 3., 5., 7.])
>>> hypergeom.ppf(prb - 1e-8, M, n, N)
array([ 0., 2., 4., 6.])
Anpassung von Verteilungen#
Die wichtigsten zusätzlichen Methoden der nicht eingefrorenen Verteilung beziehen sich auf die Schätzung von Verteilungsparametern
- fit: Maximum-Likelihood-Schätzung von Verteilungsparametern, einschließlich der Lage
und Skalierung
fit_loc_scale: Schätzung von Lage und Skalierung bei gegebenen Formparametern
nnlf: Negative Log-Likelihood-Funktion
expect: Erwartungswert einer Funktion gegen die pdf oder pmf berechnen
Leistungsprobleme und Warnhinweise#
Die Leistung der einzelnen Methoden in Bezug auf die Geschwindigkeit variiert stark je nach Verteilung und Methode. Die Ergebnisse einer Methode werden auf eine von zwei Arten erzielt: entweder durch explizite Berechnung oder durch einen generischen Algorithmus, der unabhängig von der spezifischen Verteilung ist.
Die explizite Berechnung erfordert einerseits, dass die Methode direkt für die gegebene Verteilung angegeben ist, entweder durch analytische Formeln oder durch spezielle Funktionen in scipy.special oder numpy.random für rvs. Dies sind in der Regel relativ schnelle Berechnungen.
Die generischen Methoden hingegen werden verwendet, wenn die Verteilung keine explizite Berechnung vorsieht. Zur Definition einer Verteilung ist nur eine von pdf oder cdf notwendig; alle anderen Methoden können durch numerische Integration und Wurzelfindung abgeleitet werden. Diese indirekten Methoden können jedoch *sehr* langsam sein. Als Beispiel erzeugt rgh = stats.gausshyper.rvs(0.5, 2, 2, 2, size=100) Zufallsvariablen auf sehr indirekte Weise und dauert auf meinem Computer etwa 19 Sekunden für 100 Zufallsvariablen, während eine Million Zufallsvariablen aus der Standardnormalverteilung oder der t-Verteilung etwas mehr als eine Sekunde dauern.
Verbleibende Probleme#
Die Verteilungen in scipy.stats wurden kürzlich korrigiert und verbessert und haben eine beträchtliche Testsuite erhalten; es bleiben jedoch einige Probleme bestehen
Die Verteilungen wurden über einen gewissen Bereich von Parametern getestet; in einigen Eckbereichen können jedoch einige falsche Ergebnisse verbleiben.
Die Maximum-Likelihood-Schätzung in fit funktioniert nicht mit Standard-Startparametern für alle Verteilungen, und der Benutzer muss gute Startparameter angeben. Außerdem ist die Verwendung eines Maximum-Likelihood-Schätzers für einige Verteilungen möglicherweise grundsätzlich nicht die beste Wahl.
Erstellen spezifischer Verteilungen#
Die nächsten Beispiele zeigen, wie man eigene Verteilungen erstellt. Weitere Beispiele zeigen die Verwendung der Verteilungen und einige statistische Tests.
Erstellen einer kontinuierlichen Verteilung, d.h. Unterklasse von rv_continuous#
Das Erstellen kontinuierlicher Verteilungen ist recht einfach.
>>> from scipy import stats
>>> class deterministic_gen(stats.rv_continuous):
... def _cdf(self, x):
... return np.where(x < 0, 0., 1.)
... def _stats(self):
... return 0., 0., 0., 0.
>>> deterministic = deterministic_gen(name="deterministic")
>>> deterministic.cdf(np.arange(-3, 3, 0.5))
array([ 0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1.])
Interessanterweise wird die pdf jetzt automatisch berechnet
>>> deterministic.pdf(np.arange(-3, 3, 0.5))
array([ 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
5.83333333e+04, 4.16333634e-12, 4.16333634e-12,
4.16333634e-12, 4.16333634e-12, 4.16333634e-12])
Seien Sie sich der Leistungsprobleme bewusst, die in Leistungsprobleme und Warnhinweise erwähnt werden. Die Berechnung nicht spezifizierter gemeinsamer Methoden kann sehr langsam werden, da nur allgemeine Methoden aufgerufen werden, die naturgemäß keine spezifischen Informationen über die Verteilung nutzen können. Daher, als warnendes Beispiel
>>> from scipy.integrate import quad
>>> quad(deterministic.pdf, -1e-1, 1e-1)
(4.163336342344337e-13, 0.0)
Aber das ist nicht richtig: das Integral über diese pdf sollte 1 sein. Machen wir das Integrationsintervall kleiner
>>> quad(deterministic.pdf, -1e-3, 1e-3) # warning removed
(1.000076872229173, 0.0010625571718182458)
Das sieht besser aus. Das Problem entstand jedoch dadurch, dass die pdf nicht in der Klassendefinition der deterministischen Verteilung spezifiziert ist.
Unterklasse von rv_discrete#
Im Folgenden verwenden wir stats.rv_discrete, um eine diskrete Verteilung zu erstellen, die die Wahrscheinlichkeiten der abgeschnittenen Normalverteilung für die um die ganzen Zahlen zentrierten Intervalle hat.
Allgemeine Informationen
Aus dem Docstring von rv_discrete, help(stats.rv_discrete),
„Sie können eine beliebige diskrete RV konstruieren, bei der P{X=xk} = pk gilt, indem Sie dem rv_discrete Initialisierungsmethode (über das Schlüsselwort values=) ein Tupel von Sequenzen (xk, pk) übergeben, das nur die Werte von X (xk) beschreibt, die mit einer Wahrscheinlichkeit ungleich Null (pk) auftreten.“
Daneben gibt es einige weitere Anforderungen, damit dieser Ansatz funktioniert
Das Schlüsselwort name ist erforderlich.
Die Stützstellen der Verteilung xk müssen ganze Zahlen sein.
Die Anzahl der signifikanten Ziffern (Dezimalstellen) muss angegeben werden.
Tatsächlich kann eine Ausnahme ausgelöst werden oder die resultierenden Zahlen können falsch sein, wenn die letzten beiden Anforderungen nicht erfüllt sind.
Ein Beispiel
Machen wir die Arbeit. Zuerst
>>> npoints = 20 # number of integer support points of the distribution minus 1
>>> npointsh = npoints // 2
>>> npointsf = float(npoints)
>>> nbound = 4 # bounds for the truncated normal
>>> normbound = (1+1/npointsf) * nbound # actual bounds of truncated normal
>>> grid = np.arange(-npointsh, npointsh+2, 1) # integer grid
>>> gridlimitsnorm = (grid-0.5) / npointsh * nbound # bin limits for the truncnorm
>>> gridlimits = grid - 0.5 # used later in the analysis
>>> grid = grid[:-1]
>>> probs = np.diff(stats.truncnorm.cdf(gridlimitsnorm, -normbound, normbound))
>>> gridint = grid
Und schließlich können wir rv_discrete unterklassifizieren
>>> normdiscrete = stats.rv_discrete(values=(gridint,
... np.round(probs, decimals=7)), name='normdiscrete')
Jetzt, da wir die Verteilung definiert haben, haben wir Zugriff auf alle gemeinsamen Methoden diskreter Verteilungen.
>>> print('mean = %6.4f, variance = %6.4f, skew = %6.4f, kurtosis = %6.4f' %
... normdiscrete.stats(moments='mvsk'))
mean = -0.0000, variance = 6.3302, skew = 0.0000, kurtosis = -0.0076
>>> nd_std = np.sqrt(normdiscrete.stats(moments='v'))
Testen der Implementierung
Lassen Sie uns eine Zufallsstichprobe generieren und die beobachteten Häufigkeiten mit den Wahrscheinlichkeiten vergleichen.
>>> n_sample = 500
>>> rvs = normdiscrete.rvs(size=n_sample)
>>> f, l = np.histogram(rvs, bins=gridlimits)
>>> sfreq = np.vstack([gridint, f, probs*n_sample]).T
>>> print(sfreq)
[[-1.00000000e+01 0.00000000e+00 2.95019349e-02] # random
[-9.00000000e+00 0.00000000e+00 1.32294142e-01]
[-8.00000000e+00 0.00000000e+00 5.06497902e-01]
[-7.00000000e+00 2.00000000e+00 1.65568919e+00]
[-6.00000000e+00 1.00000000e+00 4.62125309e+00]
[-5.00000000e+00 9.00000000e+00 1.10137298e+01]
[-4.00000000e+00 2.60000000e+01 2.24137683e+01]
[-3.00000000e+00 3.70000000e+01 3.89503370e+01]
[-2.00000000e+00 5.10000000e+01 5.78004747e+01]
[-1.00000000e+00 7.10000000e+01 7.32455414e+01]
[ 0.00000000e+00 7.40000000e+01 7.92618251e+01]
[ 1.00000000e+00 8.90000000e+01 7.32455414e+01]
[ 2.00000000e+00 5.50000000e+01 5.78004747e+01]
[ 3.00000000e+00 5.00000000e+01 3.89503370e+01]
[ 4.00000000e+00 1.70000000e+01 2.24137683e+01]
[ 5.00000000e+00 1.10000000e+01 1.10137298e+01]
[ 6.00000000e+00 4.00000000e+00 4.62125309e+00]
[ 7.00000000e+00 3.00000000e+00 1.65568919e+00]
[ 8.00000000e+00 0.00000000e+00 5.06497902e-01]
[ 9.00000000e+00 0.00000000e+00 1.32294142e-01]
[ 1.00000000e+01 0.00000000e+00 2.95019349e-02]]
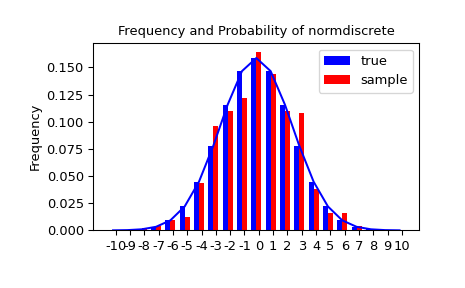
Als Nächstes können wir einen Chi-Quadrat-Test, scipy.stats.chisquare, verwenden, um die Nullhypothese zu testen, dass die Stichprobe gemäß unserer Norm-diskreten Verteilung verteilt ist.
Der Test erfordert, dass in jeder Zelle eine Mindestanzahl von Beobachtungen vorhanden ist. Wir kombinieren die Schwanzzellen zu größeren Zellen, damit sie genügend Beobachtungen enthalten.
>>> f2 = np.hstack([f[:5].sum(), f[5:-5], f[-5:].sum()])
>>> p2 = np.hstack([probs[:5].sum(), probs[5:-5], probs[-5:].sum()])
>>> ch2, pval = stats.chisquare(f2, p2*n_sample)
>>> print('chisquare for normdiscrete: chi2 = %6.3f pvalue = %6.4f' % (ch2, pval))
chisquare for normdiscrete: chi2 = 12.466 pvalue = 0.4090 # random
Konzeptionell ist die Teststatistik chi2 empfindlich gegenüber Abweichungen zwischen den Häufigkeiten von Beobachtungen und ihren erwarteten Häufigkeiten unter der Nullhypothese. Der p-Wert ist die Wahrscheinlichkeit, Stichproben aus der hypothetischen Verteilung zu ziehen, die eine Teststatistik erzeugen würden, die extremer ist als die von uns beobachtete. Unsere Teststatistik ist nicht sehr hoch; tatsächlich besteht eine 40,9%ige Chance, dass die Statistik höher als 12,466 wäre, wenn wir eine Stichprobe derselben Größe aus der diskreten Verteilung ziehen würden, die von p2 definiert wird. Daher liefert der Test wenig Beweise gegen die Nullhypothese, dass die Stichprobe aus unserer Norm-diskreten Verteilung gezogen wurde.